Теорема о равновесии плоской системы трех непараллельных сил
Теорема. Если свободное твердое тело находится в равновесии под действием плоской системы трех непараллельных сил, то линии действия этих сил пересекаются в одной точке.
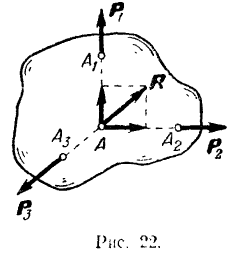
Доказательство. Пусть к телу в точках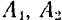 
и 
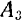приложены три непараллельные взаимно уравновешивающиеся силы 
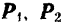и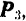 
, расположенные в одной плоскости (рис. 22). Так как данные силы не параллельны и лежат в одной плоскости, то линии действия двух из них, например 
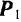и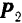 
. непременно пересекаются в какой-нибудь точке 
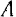. Перенеся силы 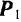и 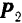по линиям действия в точку 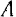и сложив их по правилу параллелограмма, получим равнодействующую силу 
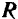. Теперь можно считать, что на тело действуют только две силы: 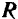и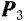 
. Эти силы должны быть направлены по одной прямой в противоположные стороны, так как по условию данные силы уравновешиваются. Следовательно, линия действия силы 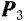должна проходить через точку 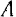, в которой пересекаются линии действия сил 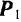и .
Доказанное условие является необходимым, по недостаточным условием равновесия трех непараллельных сил. Из того, что линии действия трех каких-либо сил пересекаются в одной точке, не следует обязательно, что эти силы находятся в равновесии.
Пользуясь данной теоремой, иногда бывает удобно определить направление реакции связи. Так, например, если стержень 
(рис.23) находится в равновесии под действием приложенных к нему активных сил и 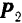и реакции 
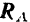шарнира 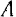, то линия действия этой реакции должна проходить через точку пересечения 
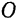линий действия сил 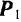и .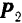
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
