Оглавление:



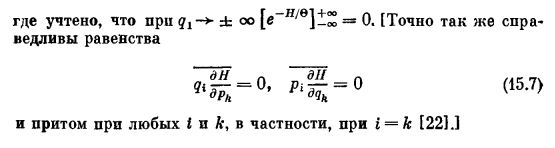

Теорема о равномерном распределении кинетической энергии по степеням свободы
Доказапные выше общие теоремы, выясняющие термодинамическое значение величин Ч’ и 0 в каноническом распределении, сохраняются в соответственно измененном виде и в квантовой статистике. Теорема о равномерном распределении, к выводу которой мы сейчас перейдем, имеет место только в классической статистике. Она позволяет дать гораздо более простое истолкование понятия температуры — именно как удвоенной средней кинетической энергии, приходящейся на одну степень свободы.
Поэтому она чрезвычайно полезна при решении вопросов, касающихся теплоем- кости тел. Людмила Фирмаль
Как указано, однако, это толкование температуры в противоположность общему ее определению как модуля канонического распределения годится только в рамках классической статистики; в квантовой же статпстике такое толкование невозможно. Теорема о равномерном распределении позволяет во многих случаях очень просто находить значение эпергпп системы в ее зависимости от температуры, значительно проще, чем путем общего метода — нахождения интеграла состояний и затем применения соотношений (11.10) и (11.11).
- Будем предполагать, что путем соответствующего выбора координат кинетическая энергия системы представлена в виде (15.1) где mi зависят от масс частиц, кроме того, они, вообще говоря, также функции координат. В прямоугольной системе координат, очевидно, — просто масса. В сферической же системе, например, для случая одной материальной точки mᵣ = т, т,— mr¹ sin’ О, т ₅ = mr. Теорема о равномерном распределении состоит в том, что средняя кинетическая энергия, приходящаяся на одну степень свободы, т. е.
Величина р*/2ггц, одинакова для всех степеней свободы и определяется только температурой согласно равенству (15.2) Мы докажем несколько более общее положение, кажем, что _____ а именно, по- 1 дН е 2р’ар₍ 2″ (15.3) Ясно, что если Н — К+ U(q) и К имеет вид (15.1), то pt дН/др^ = p*i/mi и (15.3) обращается в (15.2). Среднее от pₜ дН/др, равно Р. d₄ₗ… dqₙ dPₗ… dpₙ~ = ev ® J … Jdgj… dqₙdp, … dpₙ | e~H, ep,^dpₜ. Интеграл по р, можно взять по частям: ’■V*- — — е [^<«»15 + е ( (15.4) гораздо быстрее член в квадрат- Величина е_н/в стремптся к нулю при р, -*■ ±°° (как чем р, возрастает; следовательно, пых скобках обращается в нуль.
При выводе соотношения (15.3) мы нигде не пользовались тем, что р, — импульс. Людмила Фирмаль
Поэтому = ⁶ J • • • «WPi • • ■ dPne⁽T Н⁾/в = 6, так как интеграл в силу нормировки вероятности равен единице. Значение 1 = 1 мы взяли произвольно. То же выражение мы получили бы для любого I. Таким образом, (15.3) доказано. Существенно было только, чтобы квадратная скобка в (15.4) равнялась пулю. Поэтому если при возраста- вии координат И тоже возрастает достаточно быстро, то и для производных по координатам имеется равенство, аналогичное (15.3), а именно [211: __ (15.5) Это условие выполнено, например, для осциллятора.
Для него я =* У (m + Так ЧТ⁰ ⁽¹⁵’⁵⁾ дает⁼ Я ⁼ Т Подобным же образом, если выполнено указанное условие, легко доказать равенства ^1-0- (15.6) где I т® к. Действительно, поступая подобно прежнему, находим, например, где учтено, что прп qₜ -*■ ± оо [е = 0.
Смотрите также:

