Теорема о работе равнодействующей
Теорема. Работа равнодействующей нескольких сил на некотором пути равна алгебраической сумме работ составляющих сил на том же пути.
Пусть к материальной точке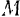 
, перемещающейся m положения 
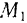в положение 
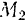по любой криволинейной траектории, приложено несколько сил
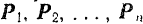
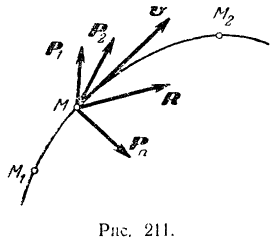
(рис. 211). Равнодействующую данных сил обозначим через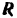 
. Приняв за ось проекций ось, имеющую направление скорости 
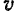точки приложения силы, будем иметь:
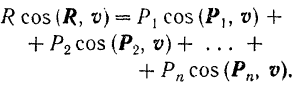
Умножая обе части равенства на элементарное перемещение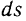 
точки приложения сил и интегрируя полученное выражение в соответствующих пределах вдоль дуги 
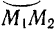, получим:
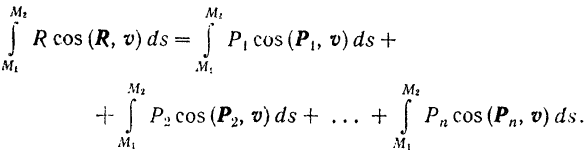
Так как интегралы в обеих частях последнего равенства представляют собой согласно формуле (190) выражения работы соответствующих сил на конечном перемещении точки приложения этих сил, то теорема доказана.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Работа силы на конечном пути с примером решения |
| Графический способ вычисления работы |
| Работа силы тяжести с примером решения |
| Работа силы упругости |
