Оглавление:
Теорема о проекциях скоростей двух точек фигуры
Теорем. Проекции скоростей Опух точек фигуры на прямую, соединяющую эти точки, равны между собой.
Доказательство. Принимая какую-либо точку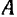 
фигуры за полюс (рис. 148), получаем для скорости другой произвольной точки 
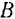фигуры следующее векторное равенство (формула (100):
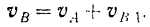
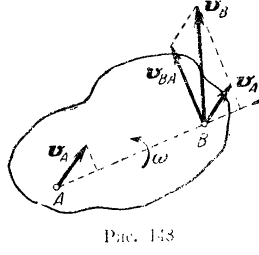
Проектируя векторы, входящие в обе части данного равенства, на прямую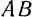 
, находим
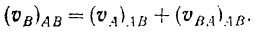
Но вектор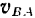 
скорости точки 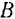относительно точки 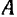перпендикулярен к отрезку 
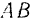и потому его проекция па прямую 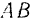равна пулю, т е.
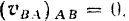
Таким образом, получаем, что
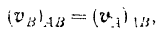
и теорема доказана.
Пример задачи:
Прямолинейный отрезок 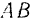движется в плоскости, причем скорости его концов образуют с прямой 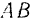углы 
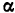и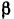 
(рис. 149). Определить скорость 
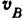, если известна скорость 
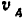точки .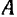
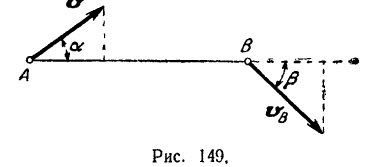
Решение:
На основании теоремы о проекциях скоростей двух точек фигуры на прямую, соединяющую эти точки, имеем
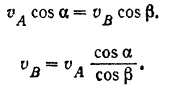
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
