Теорема о предельных вероятностях

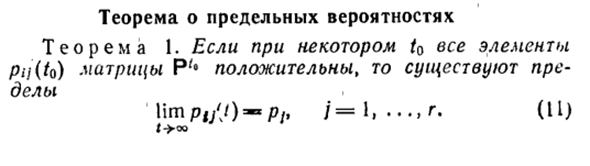
Теорема о предельных вероятностях

• Теорема о предельной вероятности Теорема 1. Для данного t0 существует ограничение, если все элементы pil (to) матрицы P ‘* положительны. lim Pi / J): m * Pb / = 1, …, d. (11) ** 00 Ограниченная вероятность pj не зависит от начального состояния i и является единственным решением системы.

• Грамм Z xkpkj = Xj, / = 1, …. r, £ * / = ■! , (12) 1 ‘/ —I Доказательство. шоу A /, (0 = rc (0, Mj (/) = min Pc (O- Если m, (/ Xp * / (/) <Л1 / (/) фут, то из уравнения Это продолжается для всех / (0 <L / (<+!) <L / Продолжение следует m / (0 <α / (/ + 1) <Λ * / (‘+ 1) <M / (0. Таким образом, подобно / — * оо, последовательности mj (t) и iW / (/) имеют ограничения.

Докажите, что эти пределы совпадают. Людмила Фирмаль

Пусть I и j -Ho), Pik (t + t0) = rnk (t + t0). Равенство друг от друга mk (t + / 0) -plk (t + / o) -Z Pit (to) Plk (Of J-л г » Λ (‘+ / o) = Plk (/ +’ o) = «Z Pc (to) Plk (Ot Мы получаем р Mk (t + / 0) -m * (* + / o) — £ (Pi / Co) -Pit Co)) Plk (0. Разделите сумму правого Z на сумму положительных слагаемых Z + и отрицательных слагаемых Z. тогда MA (t + J-gp (<+ к) <AU (/) Z + (P // (/ o) -P / i (к)) + 0 = Z (ri (t0) -p / t (/<,)) = Z ++ Z ~> тогда Z = = -Z +

Обозначение ZG (Pu (* o) — шт. Из условия Из теоремы, BCC отличается от <1, поэтому d = max 0 // оо Это означает утверждение (11), потому что / и * (/) <p ** (/) <{1} (/). Давайте перейдем к уравнению Pii (t + 1) = Pki до предела для tpik (i) / оо. получить г p / = Z pkpki- Я г Далее Zp / =, то есть ограниченная вероятность pi Система зарядки (12).

• Предположим, что некоторый X \ 9 gr удовлетворяет (12). Тогда они встречают любую систему т г * / = Z ** P *, (O. 04) L ™ 1 Это доказано по индукции: г г г г Z * ftPft / (‘+ 0 = Z ** Z PkiPlI (0 ~ фут-1 л — 1 1 = Z (z ^ Pft / J Pu (0 = Z xipn (0 = Когда мы достигаем предела t-> oo в (14), мы получаем == Z * lP / = P / -теорема доказана.

Из уравнения (10) в условиях теоремы I AT равен t + oo, и ограничение не зависит от начального распределения p (0). Можно подтвердить, что цепь Маркова, описывающая блуждание с отражением в примере 2, удовлетворяет условиям теоремы.

Предельные вероятности в этом случае можно найти с помощью уравнений (12). Людмила Фирмаль

Смотрите также:

Предмет теория вероятностей и математическая статистика

Марковская зависимость испытаний	Случайные величины и их распределения
Переходные вероятности	Многомерные распределения