Теорема о параллельном переносе силы. Главный вектор и главный момент произвольной системы сил
Теорема. Не изменяя действия силы на абсолютно твердое тело, ее можно перенести параллельно начальному положению в любую точку тела, прилагая при этом пару, момент которой равен моменту переносимой силы относительно той точки, куда сила переносится.
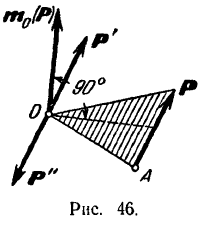
Доказательство. Пусть мы имеем силу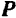 
, приложенную в точке 
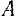тела (рис. 46). Возьмем произвольную точку 
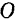тела и приложим к ней две противоположно направленные силы 
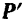и 
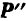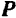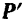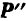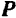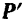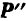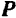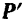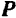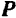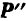, параллельные и равные по модулю силе . Так как силы и взаимно уравновешиваются, то полученная система трех сил , и эквивалентна одной силе . Сила может рассматриваться как сила , перенесенная параллельно ее начальному положению, а силы и образуют пару. Момент этой пары (рис. 46) равен моменту силы 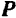относительно той точки 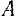, в которую сила переносится. Теорема доказана.
Рассмотрим примеры, иллюстрирующие эту теорему.
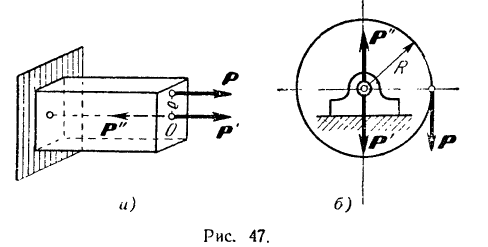
- К брусу (рис. 47, а) приложена сила 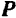, причем линия действия этой силы параллельна оси стержня и проходит от нее на расстояние
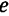. Перенесем силу 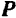параллельно ее начальному положению в центр 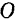тяжести, добавив при этом уравновешенную систему сил 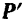, 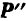. Ясно, что действие силы 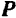на брус эквивалентно
действию на него силы 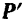, растягивающей брус, и пары 
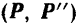, изгибающей брус. Модуль момента этой пары равен 
.
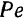- К окружности шкива (рис. 47, б) приложена сила 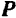, лежащая в плоскости, перпендикулярной оси вращения шкива. Шкив будет при этом воздействовать на подшипник с силой 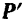, равной по модулю (если пренебречь весом шкива) и параллельной силе 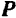. Действие же всегда равно противодействию и со стороны подшипника будет приложена к шкиву реакция 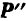подшипника, равная по модулю и прямо противоположная силе 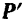. 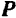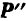Приложенные к одному телу (шкиву) силы и образуют пару, модуль момента которой равен
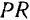. Эта пара и приводит шкив во вращение.
Теорема о параллельном переносе силы лежит в основе весьма плодотворного метода Пуансо, позволяющего приводить к одной точке (с добавлением соответствующих пар) любую систему произвольно расположенных сил. Пусть на твердое тело действует система нескольких, например, трех, сил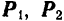 
и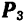 
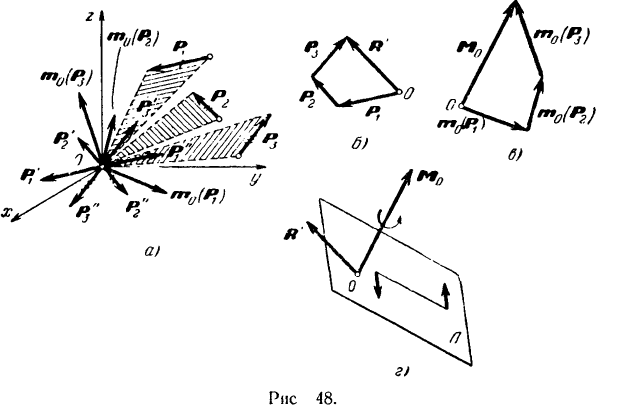
, расположенных как угодно в пространстве. Возьмем произвольную точку и перенесем в нее, пользуясь теоремой Пуансо, все силы системы. В результате мы получим (рис. 48, о) пространственную систему сил 
и 
, приложенных
к одной точке 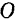, и пространственную систему присоединенных пар 
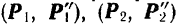и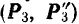 
. Для наглядности на рис. 48, а векторы сил присоединенных пар перечеркнуты соответственно одной, двумя и тремя черточками.
Приложенные к одной точке силы 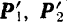и 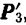мы можем сложить по правилу векторного многоугольника (рис. 48,6) и, следовательно, заменить одной, эквивалентной им, силой 
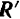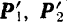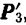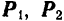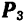. Так как силы и соответственно равны силам и , то
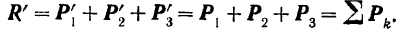
Как мы уже говорили ранее (стр. 38), вектор 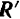, равный геометрической сумме всех сил данной системы, называется главным вектором этой системы.
Пары, расположенные как угодно в пространстве, также можно сложить и заменить одной результирующей парой, момент которой равен геометрической сумме моментов составляющих пар. Момент каждой из пар, присоединяемой при переносе сил в одну точку, равен моменту соответствующей силы относительно этой точки.
Произвольная гонка тела, в которую мы переносим параллельно самим себе все силы системы, называется центром приведения. Можно, следовательно, сказать, что момент результирующей пары равен геометрической сумме моментов всех сил системы относительно центра приведения.
Геометрическая сумма моментов всех сил системы относительно какой-либо точки называется главным моментом данной системы сил относительно этой точки.
Обозначая главный момент системы сил относительно какой-либо точки 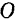символом 
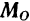, будем иметь:
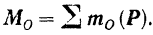
Изображая (рис. 48,о) моменты сил системы относительно выбранного центра 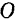приведения векторам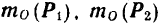и 
и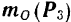 
, построенными в соответствии с установленным в предыдущем параграфе правилом, мы можем затем сложить их по способу векторного многоугольника (рис. 48, б) и тем самым найти главный момент 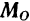данной системы сил относительно точки 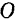, т. е. момент результирующей пары.
Таким образом, мы приходим к следующему выводу: любая система сил эквивалентна по своему действию на абсолютно твердое тело совокупности: одной силы 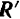, равной главному вектору данной системы и приложенной в произвольной точке тела (в центре приведения), и одной пары, момент которой равен главному моменту 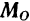данной системы сил относительно выбранного центра 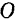приведения (рис. 48,г).
Модуль и направление главного вектора 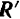системы не зависит от выбора центра приведения, так как все силы переносятся в центр приведения параллельно самим себе, и силовой многоугольник во всех случаях будет одним и тем же. Наоборот, модуль и направление главного момента 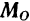зависят, вообще говоря, от выбора центра приведения, так как с изменением центра приведения изменяются модули и направления моментов сил
системы относительно этого центра, а следовательно, и их геометрическая сумма. Поэтому когда говорят о главном моменте данной системы сил, то всегда указывают, относительно какой точки он определяется.
Установив общие понятия момента пары и момента силы относительно точки, а также способ приведения произвольной системы сил к одному центру, мы перейдем сейчас к рассмотрению частного случая, когда все силы системы лежат в одной плоскости.
По чисто методическим соображениям, более детальное рассмотрение общего случая произвольной пространственной системы сил будет сделано в главе VII.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
