Теорема о моментах инерции тела относительно параллельных осей
Центральной осью называется ось, проходящая через центр масс тела.
Момент 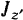 инерции тела относительно какой-либо оси
инерции тела относительно какой-либо оси 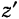 равен моменту
равен моменту 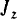 инерции этого тела относительно центральной оси
инерции этого тела относительно центральной оси 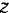 , параллельной данной оси
, параллельной данной оси 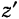 , сложенному с произведением массы
, сложенному с произведением массы 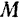 тела на квадрат расстояния
тела на квадрат расстояния 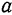 между этими осями.
между этими осями.
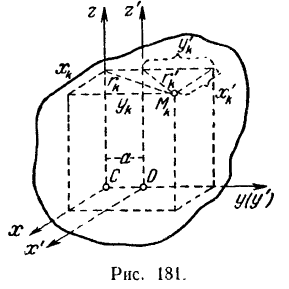
Доказательство. Примем центр 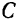 масс тела за начало системы координатных осей
масс тела за начало системы координатных осей 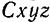 . Ось
. Ось 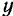 проведем так, чтобы она пересекла ось
проведем так, чтобы она пересекла ось 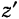 в некоторой точке
в некоторой точке 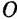 , которую примем за начало новой системы координатных осей
, которую примем за начало новой системы координатных осей 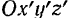 (рис. 181). Расстояние между осями
(рис. 181). Расстояние между осями 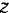 и
и 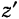 обозначим через
обозначим через 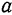 . Возьмем теперь произвольную точку
. Возьмем теперь произвольную точку 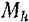 тела массы
тела массы 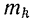 . Координаты этой точки в системе координат
. Координаты этой точки в системе координат 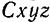 обозначим через
обозначим через 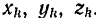 . Координаты той же точки в системе координат
. Координаты той же точки в системе координат 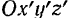 обозначим через
обозначим через 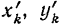 и
и 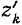 . Расстояние точки
. Расстояние точки 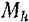 до оси
до оси 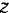 обозначим через
обозначим через 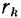 и расстояние той же точки до оси
и расстояние той же точки до оси 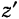 через
через 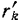 .
.
Момент инерции тела относительно оси 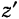 согласно определению:
согласно определению:
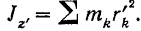
Но, как это ясно из рис. 181,
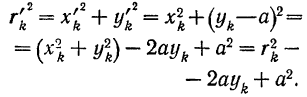
Подставляя это значение в выражение для 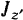 , будем иметь:
, будем иметь:
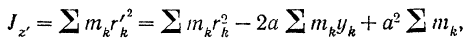
где
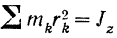
момент инерции тела относительно
центральной оси 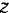
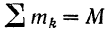
масса тела.
Из формулы же (138), определяющей ординату 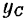 центра масс, находим:
центра масс, находим:
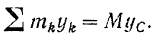
Так как в нашем случае
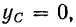
то и 2
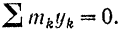
Подставляя найденные значения в правую часть равенства (I), получаем:
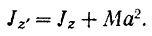
Теорема доказана.
Зная момент инерции тела относительно какой-либо центральной оси, можно, пользуясь формулой (143), найти момент инерции этого тела относительно любой другой оси, параллельной данной центральной.
Как это следует из той же формулы, момент инерции тела относительно центральной оси меньше, чем момент инерции того же тела относительно любой другой оси,ей параллельной.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

