Оглавление:
Теорема о движении центра масс системы
По теореме об изменении количества движения системы (формула (160)) имеем:
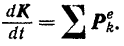
Но количество движения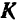 
системы можно вычислить, зная массу 
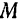системы и скорость 
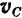ее центра 
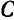масс, по формуле (151):
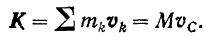
Подставляя данное выражение в предыдущее уравнение, будем иметь:
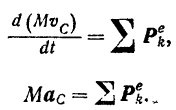
Проектируя обе части последнего векторного уравнения на оси координат и вспоминая, что проекции ускорения точки на координатные оси равны вторым производным по времени от соответствующих координат точки, получаем:
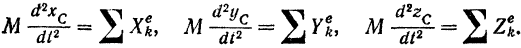
Уравнение (165) выражает собой теорему о движении центра масс в векторной форме, а уравнения (166) — ту же теорему в скалярной форме.
Сравнивая уравнение (165) с основным уравнением (106) динамики для отдельной материальной точки и уравнения (166) с дифференциальными уравнениями (111) движения точки, нетрудно сделать заключение о том, что уравнения движения центра масс системы внешне схожи с уравнениями движения отдельной материальной точки, если положить массу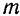 
этой точки, равной массе 
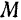всей системы и силу 
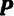, действующую на точку, равной сумме 
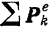всех внешних сил, действующих на систему.
Таким образом, теорему о движении центра масс системы можно сформулировать так: центр масс всякой системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.
Так как теорема о движении центра масс представляет собой лишь другую форму теоремы об изменении количества движения системы, то при решении многих задач они вполне заменяют друг друга.
Рассмотрим несколько важных следствий, вытекающих из данных теорем.
I. Поступательно движущееся тело можно рассматривать в задачах динамики как материальную точку, масса которой равна массе тела и к которой приложены все внешние силы, действующие на тело.
При поступательном движении твердого тела его центр масс движется так же, как и все остальные точки этого тела. Определив движение центра масс тела, на основании теоремы о движении этой точки, в случае поступательного движения тела, мы тем самым полностью определяем его движение.
Таким образом, при исследовании поступательного движения тела можно пользоваться, как мы это и делали уже при решении задач, всеми методами и теоремами динамики точки.
II. Закон сохранения движения центра масс.
- Если в течение некоторого времени главный вектор всех внешних сил, действующих на систему, остается равным нулю, то центр масс данной системы все это время будет оставаться в покое или двигаться прямолинейно и равномерно.
В самом деле, из уравнения (165) следует, что если
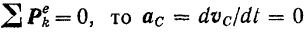
и потому
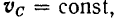
т. е. в этом случае скорость центра масс постоянна как по модулю, так и по направлению. В частности, если начальная скорость 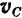центра масс была равна нулю, то центр масс будет оставаться в покое.
- Если в течение некоторого времени сумма проекций всех внешних сил, действующих на систему, на какую-либо ось остается равной нулю, то проекция скорости центра масс на данную ось все это время будет оставаться постоянной.
В самом деле, из уравнения (166) следует, что если
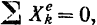
то
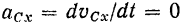
и потому
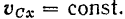
В частности, если в начальный момент проекция на эту ось скорости центра масс
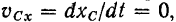
то соответствующая координата центра масс будет оставаться постоянной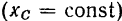 
.
III. Внутренние силы системы-при отсутствии внешних сил не могут изменять движения центра масс системы, так же как не могут (стр. 299) изменять и общего количества движения системы.
Отсутствие внутренних сил в уравнениях, выражающих теоремы о движении центра масс системы и об изменении ее количества движения, придает этим теоремам большую практическую ценность, так как позволяет исключать из рассмотрения неизвестные внутренние силы. Отсюда следует, что, применяя эти теоремы к решению конкретных задач, надо стараться выбирать за систему такую совокупность точек (или тел), чтобы ряд неизвестных сил оказались для нее внутренними силами.
Рассмотрим некоторые примеры, иллюстрирующие данные положения.
- Так как притяжением звезд, внешних по отношению к телам Солнечной системы, можно практически пренебречь, то Солнечную систему в первом приближении можно рассматривать как «изолированную» систему, на которую не действуют никакие внешние силы. Отсюда следует, как это и показали соответствующие наблюдения, что центр масс Солнечной системы движется прямолинейно и равномерно относительно системы «неподвижных» звезд. Поэтому гелиоцентрическая система координат, о которой было сказано во введении (стр. 235), представляет собой практически инерциальную систему отсчета.
- Человек, стоящий на абсолютно гладкой горизонтальной поверхности, не может сам передвинуться в горизонтальном направлении. Внешними силами для системы, которую представляет собой человек, будут вес человека и нормальная реакция гладкой горизонтальной плоскости. Обе эти силы вертикальны, и потому сумма их проекций на любую горизонтальную ось равна нулю. Следовательно, равна нулю и проекция ускорения центра тяжести человека на эту ось. Если человек вначале стоял неподвижно, то из-за отсутствия горизонтальных внешних сил горизонтальная скорость его центра тяжести будет оставаться равной нулю и в дальнейшем. Никакими внутренними усилиями нельзя переместить центр тяжести системы. Как только человек вынесет вперед одну ногу, другая нога сейчас же отодвинется назад и, следовательно, его общий центр тяжести будет оставаться на месте. В действительных условиях хождение человека по горизонтальной плоскости возможно только благодаря внешней горизонтальной силе, возникающей вследствие трения между этой плоскостью и подошвами ног. Когда человек выносит одну ногу вперед, другая стремится назад, но этому мешает трение подошвы ног о плоскость, почему последняя остается на месте (или почти на месте).
Аналогичным образом объясняется и движение в горизонтальном направлении паровоза, автомобиля и т. д. Давление пара на поршень машины есть, по отношению к паровозу, внутренняя сила и потому не может сообщить движение его центру масс. Движение поезда возможно лишь благодаря трению между рельсами и ведущими колесами паровоза (т. е. колесами, приводимыми в движение паровой машиной).
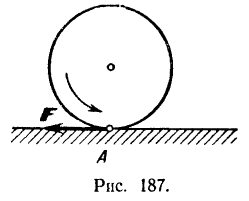
Если ведущее колесо будет вращаться так, как показано на рис. 187, то точка 
касания колеса с рельсом будет скользить вправо и, следовательно, на нее будет действовать сила трения 
, направленная влево. Эта внешняя для паровоза сила (если она достаточна для преодоления сопротивления его движению со стороны ведомых колес) и будет перемещать центр масс паровоза в ту же сторону, т. е. влево. При отсутствии достаточного сцепления ведущих колес с рельсами они будут вращаться на месте (буксовать).
Выше мы говорили о том, что внутренние силы системы не могут сами изменять движение ее центра масс и общее количество движения системы. Однако из рассмотренных примеров видно, что, вызывая движение отдельных частей системы и их воздействие на окружающие систему внешние тела и материальную среду, они могут вызывать возникновение внешних для данной системы сил, которые будут изменять движение центра масс системы и ее общее количество движения.
- Пусть пара сил
приложена к неподвижному твердому телу (рис. 188), имеющему возможность свободно перемещаться параллельно плоскости действия пары.
Геометрическая сумма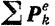 
сил пары равна нулю и потому, как это следует из закона сохранения движения центра масс, она не может сообщать ускорения
центру 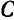тяжести тела, и он, следовательно, должен оставаться неподвижным. Этим и объясняется то, указанное еще в статике (§ 16) обстоятельство, что пара сил всегда сообщает свободному твердому телу вращение вокруг оси, перпендикулярной к плоскости действия нары и проходящей через центр тяжести тела.
Пример задачи:
Из орудия весом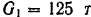 
, расположенного на гладкой горизонтальной платформе (рис. 189), вылетает со скоростью 
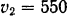м/сек снаряд весом 
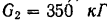. Ствол орудия образует с горизонтом угол 
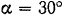. Определить скорость 
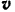орудия после выстрела (скорость свободного отката).
Решение:
Будем рассматривать снаряд и орудие как одну систему. Это позволяет при решении задачи исключить из рассмотрения давление пороховых газов в канале ствола орудия, которое будет для данной системы внутренней силой. Внешними силами для этой системы будут только: силы тяжести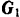 
орудия и 
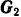—снаряда и нормальная реакция 
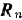платформы. Эти внешние силы вертикальны и потому сумма 
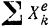их проекций на горизонтальную ось 
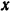равна нулю. В этом случае согласно условию (164);
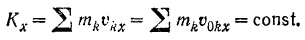
До выстрела система была неподвижна, и потому
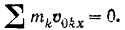
Отсюда следует, что и после выстрела проекция на ось 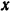(направление которой показано па рис. 189) количества движения систем и должна равняться нулю:
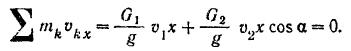
Из этого равенства находим проекцию на ось 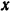искомой скорости отката орудия:
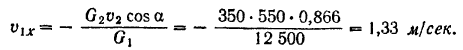
Знак минус в выражении проекции скорости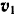 
отката орудия указывает на то, что эта скорость направлена в сторону, противоположную горизонтальной составляющей скорости 
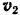снаряда.
Пример задачи:
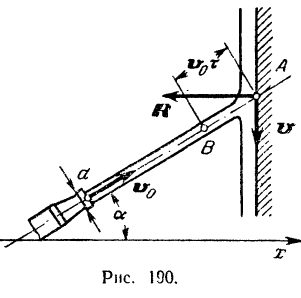
Из наконечника диаметром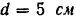 
бьет струя воды под углом 
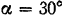к горизонту со скоростью 
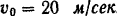. Определить силу давления струи на близстоящую вертикальную стену (рис. 190), пренебрегая действием силы тяжести на форму струи и считая, что после встречи со стеной все частицы жидкости движутся вдоль стены.
Решение:
Частицы жидкости производят давление на стену, которое вызывает равную и противоположно направленную реакцию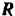 
стены, приложенную к частицам жидкости. Так как мы принимаем, что после встречи со стеной частицы жидкости свободно стекают по ней, то реакцию 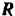стены можно считать направленной по нормали к ней. При большой скорости струи остальные внешние силы, действующие на частицы жидкости, малы сравнительно с реакцией стены и ими можно пренебречь.
Применим к движению струи теорему об изменении проекции количества движения системы (в конечной форме).
По уравнению (162)
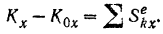
Рассмотрим движение струи за малый промежуток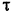 
времени. За систему примем находящийся около стены объем струи, соответствующий малому ее отрезку 
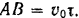. Масса этой системы 
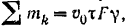где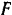 
— площадь поперечного сечения струи, 
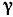— плотность.
В момент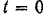 
все частицы струи имеют одинаковую скорость 
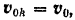, направленную под углом 
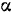к горизонтальной оси 
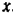. Следовательно,
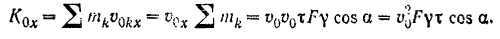
По истечении промежутка 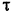времени все частицы выделенного объема струи будут находиться на стене и иметь скорость 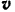, направленную вдоль стены, т. е. перпендикулярную к горизонтальной оси 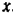. Следовательно,
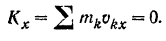
Так как на нашу систему действует только одна внешняя сила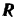 
и ее проекция на ось 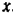равна —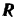, то в данном случае сумма
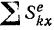
проекций импульсов внешних сил за рассматриваемый промежуток 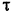времени будет равна
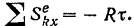
Таким образом, уравнение (162) применительно к движению данной системы будет иметь вид
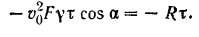
Отсюда реакция стены (равная по модулю искомой силе давления струн на стену) будет равна
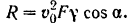
Для вычисления значения модуля реакции воспользуемся системой СИ. Начальная скорость струи
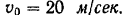
Площадь ее сечения
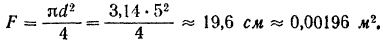
Так как объем струи будет выражен в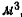 
, то за плотность воды надо принять массу 1 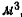, т. е.
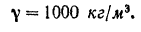
Подставляя эти данные, получим
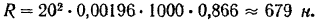
Если нам желательно выразить силу давления струп в кГ, го для этого надо умножить силу в ныотонах на 0,102:
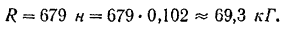
Пример задачи:
Ножницы для резки металлов состоят из кривошипно-шатунного механизма 
, к ползуну 
которого прикреплен подвижный нож; неподвижный нож укреплен на фундаменте 
(рис. 191). Пренебрегая массой шатуна и считая кривошип однородным стержнем, определить давление фундамента на грунт при холостом ходе ножа. Кривошип вращается с постоянной угловой скоростью. Дано: длина кривошипа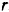 
, длина шатуна 
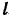угловая скорость кривошипа 
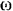, вес фундамента и корпуса 
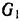, вес кривошипа 
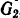, вес ползуна с ножом 
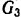. В начальный момент кривошип занимал вертикальное нижнее положение.
Решение:
Примем ножницы вместе с фундаментом за систему. Внешними силами, действующими на эту систему, будут силы тяжести: 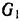— корпуса с фундаментом, 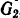— кривошипа, 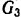— ползуна с ножом и 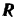— нормальная реакция грунта.
Направим ось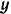 
вертикально вниз, взяв за начало координат неподвижную точку 
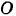на оси вращения кривошипа, и напишем дифференциальное уравнение (166) движения центра масс нашей системы:
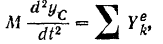
где
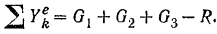
Ордината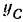 
центра масс системы находится по формуле (138):
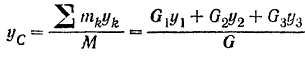
где
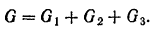
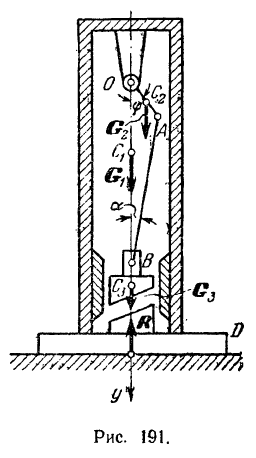
При равномерном вращении кривошипа угол его поворота
Ордината центра тяжести кривошипа
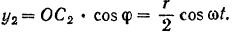
Ордината центра тяжести ползуна с ножом:
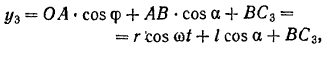
где
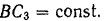
Наконец, ордината центра тяжести корпуса ножниц с фундаментом:
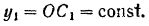
Выразим угол 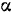как функцию времени. По теореме синусов
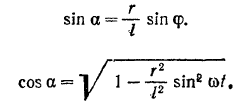
Выражение для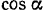 
разложим в ряд. Так как 
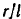— правильная дробь, то, отбрасывая члены ряда, содержащие 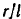в степени выше второй, получим:
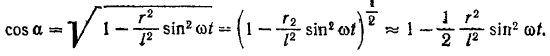
Отсюда
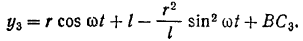
Подставляя значения 
и 
в формулу для ординаты центр I масс, будем иметь:
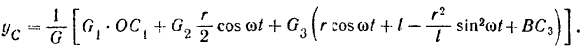
Дважды дифференцируя это выражение по времени, найдем:
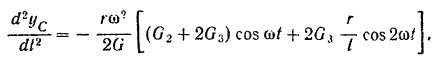
Подставляя значения (III) и (II) в уравнение (I), получим:
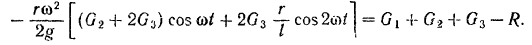
Отсюда находим искомую нормальную реакцию грунта:
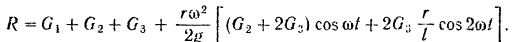
Момент количества движения точки относительно центра и относительно оси
Понятия момента относительно центра и относительно оси, установленные в статике для силы, могут быть применены к любым векторам, в частности, и к количеству движения материальной точки.
В ряде случаев движение материальной точки оказывается удобней характеризовать не изменением количества движения точки, а изменением его момента относительно какого-либо центра или какой-либо оси. Эти моменты будут учитывать уже не только модуль и направление количества движения точки, но и положение самой точки относительно данного центра или данной оси.
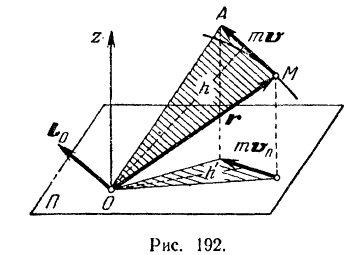
Определяется момент количества движения материальной точки совершенно так же, как и момент силы. Отметим положение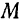 
движущейся материальной точки и ее количество движения 
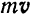в данный момент времени (рис. 192).
Момент количества движения mv материальной точки 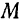относительно какого-либо центра 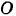есть вектор 
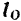(рис. 192), перпендикулярный к плоскости 
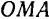, в которой расположены вектор mv и центр моментов 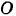, и направленный в такую сторону, откуда вектор 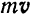относительно центра моментов представляется направленным против хода стрелки часов.
Модуль 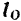момента количества движения точки относительно центра равен произведению модуля количества
движения точки на плечо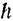 
, т. е. на кратчайшее расстояние от центра моментов до линии, на которой лежит вектор :
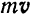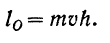
Подобно тому как и момент силы относительно центра (стр. 68), момент количества движения материальной точки 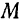относительно какого-либо центра 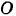может быть выражен в виде векторного произведения радиуса-вектора 
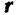(рис. 192) этой точки относительно данного центра на ее количество движения:
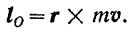
Аналогично соответствующему понятию статики (стр. 108) проекция момента 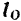количества движения точки относительно какого-либо центра на любую ось 
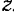, проходящую через этот центр, называется моментом 
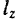количества движения точки относительно этой оси:
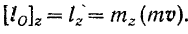
Совершенно так же, как это было сделано в статике (§ 32), можно доказать, что момент 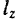количества движения материальной точки относительно оси 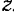равен алгебраической величине момента проекции 
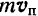количества движения этой точки на плоскость 
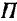, перпендикулярную к оси 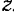относительно точки пересечения оси с этой плоскостью (рис. 192):
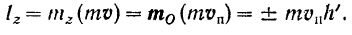
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
