Теорема о движении центра масс
Иногда, чтобы оценить движение материальной системы в целом, достаточно определить движение какой-нибудь одной ее точки. Например, если бросить камень в цель, совсем не нужно знать, как он будет кувыркаться во время полета, важно установить, попадет он в цель или нет. Для этого достаточно рассмотреть движение какой-нибудь точки этого тела.
Оказывается, довольно просто можно определить движение центра масс материальной системы. Составим для каждой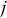 
-й точки материальной системы основное уравнение динамики (12.2), разделив силы, действующие на точки, на внешние и внутренние:
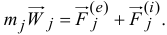
Затем сложим эти уравнения:
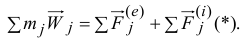
Вторую сумму в правой части равенства можно отбросить, так как векторная сумма внутренних сил равна нулю. Левую часть можно записать иначе. Так как радиус-вектор центра масс (см. 14.1)
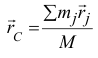
то
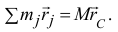
Взяв вторую производную по времени (полагая массу постоянной), получим
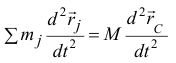
или
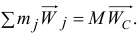
Подставив эту сумму в левую часть равенства (*), получим
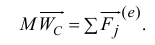
Спроектируем это векторное равенство на оси координат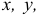 
и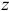 
. Вспоминая, что проекции вектора ускорения 
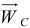на оси есть вторые производные по времени от координат точки, получим дифференциальные уравнения движения центра масс
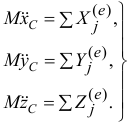
Сравнивая эти уравнения с дифференциальными уравнениями движения материальной точки (13.1) и уравнение (19.1) с основным уравнением динамики (12.1), можно сформулировать закон движения центра масс.
Движение центра масс материальной системы определяется так же, как движение материальной точки, масса которой равна массе всей системы, под действием внешних сил, приложенных ко всем точкам системы.
Теорема о движении центра масс позволяет сделать несколько важных замечаний.
Первое. Внутренние силы не могут изменить движение центра масс системы. Они вызывают движение лишь отдельных тел и точек системы.
Так, движение автомобиля по горизонтальной плоскости может происходить только под действием внешних сил, равных силам трения, действующих на колеса со стороны дороги. И торможение автомобиля тоже возможно только этими силами, а не трением между тормозными колодками и тормозным барабаном. Если дорога гладкая, то как бы тормозные колодки не затормаживали колеса, они будут скользить и не остановят автомобиль.
Или после взрыва летящего снаряда (под действием внутренних сил) части, осколки его разлетятся так, что центр масс их будет двигаться по прежней траектории.
Второе. Если внешние силы на систему не действуют или действуют, но сумма их равна нулю, то центр масс системы будет либо находиться в покое, либо двигаться равномерно и прямолинейно, так как ускорение центра масс равно нулю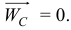 
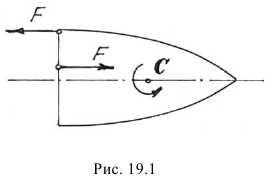
Например, если на тело начнут действовать две силы, образующие пару сил (рис. 19.1), то центр масс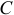 
его будет двигаться по прежней траектории. А само тело будет вращаться вокруг центра масс. И неважно, где приложена пара сил. Кстати, в статике мы доказывали, что действие пары сил на тело не зависит от того, где она приложена. Здесь мы показали, что вращение тела будет вокруг центральной оси .
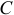Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Уравнения равновесия Лагранжа |
| Обобщенные силы инерции в теоретической механике |
| Теорема об изменении количества движения |
| Теорема об изменении момента количества движения |
