Оглавление:



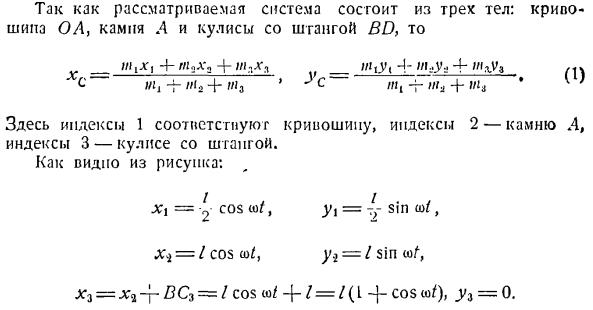










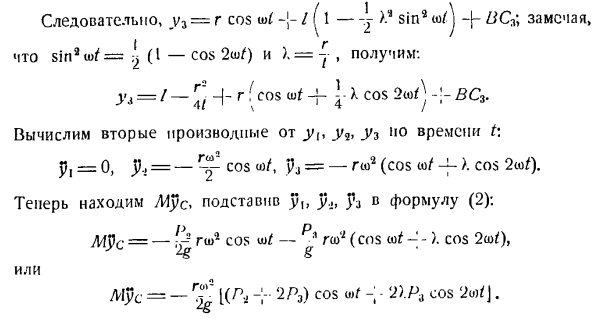



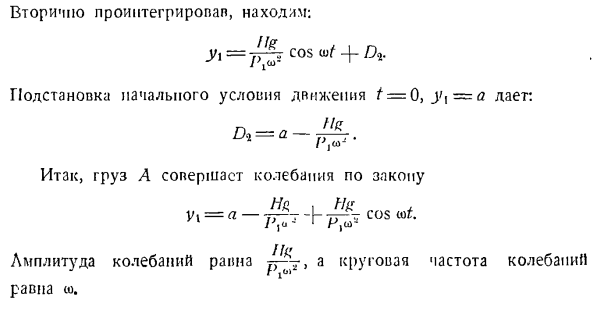


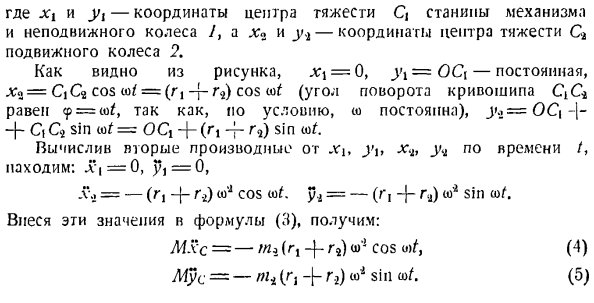



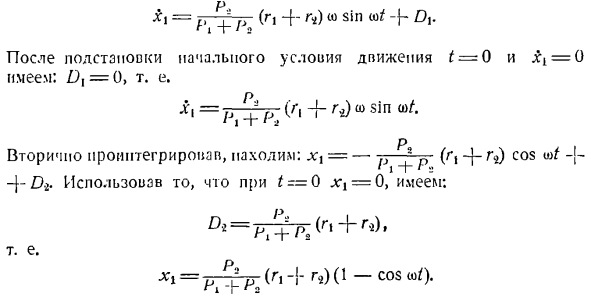



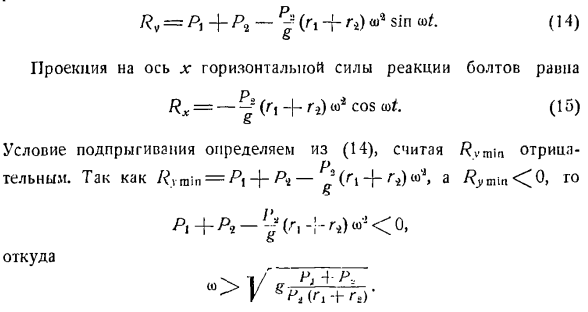














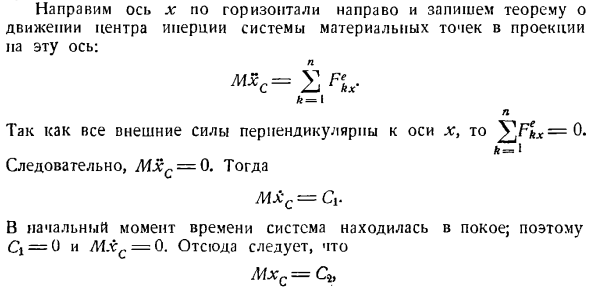



Теорема о движении центра инерции системы материальных точек
- Теорема о движении центра инерции материальной точечной системы 1°.Инерционная система материальной точечной системы. Центром инерции (центра тяжести) материальной точечной системы является точка, в которой положение определяется радиусом радиуса РК. На движение центра инерции системы это не влияет. Этот факт значительно облегчает решение задачи, так как внутренние силы системы, в значительной степени неизвестны.
Задача динамики поступательного движения твердых тел решается теоремой о движении центра инерции материальной точки system. In факт, мы применяем эту теорему для определения уравнения траектории, скорости и ускорения твердого тела centroid. При решении задач с динамикой рекомендуется, чтобы полюса системы были центром инерции материальных точек, когда движение точек в системе разложено на поступательное направление относительно полюсов и полюсов.
In при поступательном движении твердого тела траектории всех точек одинаковы, а их скорости и ускорения равны соответственно. Людмила Фирмаль
Затем, применив теорему к движению центра инерции, можно определить подвижное поступательное движение точек системы. Следующее можно решить с помощью теоремы о движении центра инерции: 1) прямая задача, в которой задаются законы движения отдельных важных точек и их масс и ищутся внешние силы. 2) закон движения всех точек системы задается обратной задачей (кроме 1 (или закон движения некоторых точек представлен законом неизвестного движения этой точки), определяются масса точек системы и движение 1 точки.
Для решения задачи рекомендуется использовать теорему о движении инерциального центра системы критических точек следующей последовательности Эл. 1) на рисунке показаны все внешние силы системы. 2) Выберите систему координат. 3) Напишите теорему о движении центра инерции системы материальных точек в проекции на ось декартовых координат: МХ = С П *. Туалет = £ Фив м! C = £ Fi、 м-я к-я к = I 4) вычислить сумму проекций всех внешних сил системы на оси декартовых координат. 5) запишите координаты центра инерции всех n масс системы xb> yk> 2k>here= = 1> 2, I, и после дифференцирования их 2 раза во времени используйте формулу для определения Mho Mus и M2c: ССХ = в ТХ «МУС = ±mhy», AVJC = м»?Лейтенант к-1 л-и
- Если система содержит тело с непрерывным распределением масс, то необходимо описать центры координат xk, yk n zk Тяжесть этих органов и почему делают мхэ, вычисляют Афжта по приведенной выше формуле(среди них йод/ 7 / d. It надо уже понимать массу арт-тела); Ж) используя полученные результаты, запишите дифференциальное уравнение движения центра инерции системы, приложенное к этой системе (3-й толчок). 7) непосредственно определить искомую внешнюю силу системы при решении задачи или найти искомый закон движения, который равен 1 центроиду массы системы при решении обратной кинематической задачи.
Задача 263.Когда снаряд летит в безвоздушном пространстве, центр инерции снаряда рисует параболу. Меняется ли орбита инерциального центра, когда снаряд взрывается в полете с каким-то обломком? Решение. Оболочка разрывается под действием внутренних сил, которые непосредственно не влияют на движение центра инерции корпуса. system. . Задача 264.Какова мощность привода центра автомобиля, движущегося по неровной горизонтальной дороге? Проблема 2G4 для. Solution.
As в результате осколки снаряда должны двигаться так, чтобы центр инерции лопнувшего снаряда двигался по той же траектории, то есть по параболе Людмила Фирмаль
In во многих случаях атомный инерционный центр шипа непосредственно полезен, и движение давления газа ошибочно принимается за 15 цилиндров двигателя. Эта сила в салоне напрямую не влияет на движение центра инерции автомобиля. Под действием этой силы пара сил, приложенных к ведущим колесам, генерирует torque. As в результате возникает сила трения F ^между шиной ведущего колеса и грунтом автомобиля, и она направлена горизонтально в направлении движения автомобиля(сила трения между шиной ведущего колеса и грунтом игнорируется).
Сила трения, которая является внешней по отношению к автомобилю, перемещает его центр инерции C. In дело в том, что если записать теорему о движении центра инерции системы в проекции на ось x (см. рисунок), то Mxe-> mp(внешние силы I, Z и K. 2 PSR » идеально соответствует оси x, а проекция этой оси равна нулю), то есть xc0.Если в первый момент центр инерции с неподвижен, то он движется горизонтально, ускоряясь вправо.
Задача 265.Если центр тяжести диска находится на его оси вращения, определите основной вектор Ve внешних сил, приложенных к равномерному диску, вращающемуся вокруг неподвижной оси. Решение. Применим теорему к движению центра инерции н Точечная система Mwc = ^ Fek. It это центр тяжести. к-1П Если диск фиксирован, то wc = 0, следовательно^ F * = VC = 0, т. е. м-я Главный вектор внешней силы, приложенной к диску(включая силу реакции сцепления), равен пуле. Выпуск 266.Длина / и масса Р рыхлый, однородный стержень ОА вращается вокруг вертикальной оси 0 \ 0r с постоянной угловой скоростью а).Определите основной вектор внешних сил. Масса оси 0 (h игнорируется. Решение.
Согласно теореме о движении центра инерции материальной системы н Фактическая точка= ^ Fek \ onpt- Нынешнего века разделение внешних сил Юрского ч- Больше Достаточно найти систему Ve = V ^ Центр инерции стержня находится в точке с расстояния^от оси вращения, а по постоянству вектора 0) центростремительное ускорение wn = = OS * * = ω » 2, направленный от C до O вдоль стержня, то основной вектор > 1 Ноги Один Два О, и/.Да. Один И Меня, меня. Вау. Перейдите к задаче 260. Направление силы системы V одинаково, а величина равна С- (В этом случае главным вектором внешних сил является векторная сумма веса стержня и сил реакции опоры Ot и () 2.)
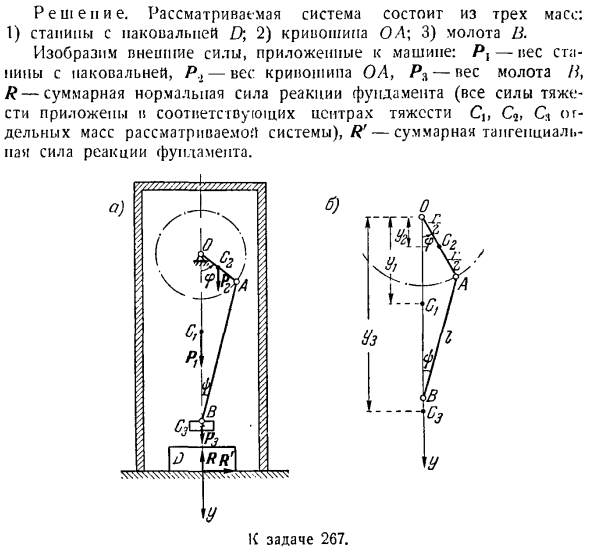
Выпуск 267.Ковочная машина для металла (см. рисунок а) приводится в движение кривошипно-шатунным механизмом OAB. если paOoie простаивает, то вес кровати с наковальней I) равен Plt, тогда определите давление машины на учредительство. Вес длины R кривошипа OA равен весу гомолога B. Это будет равно R. Кривошип, вращающийся против часовой стрелки с постоянной угловой скоростью с, первоначально занимал нижнее вертикальное положение. Масса шатуна A B длины I игнорируется.
Решение. Рассматриваемая система состоит из 3 масс: 1) станина с наковальней D 2) кривошип OL \ 3) молоток B. Поясним внешнюю силу, приложенную к машине: масса станины с Ru-наковальней R.-масса кривошипа ОА, масса ПК-молота в, р-суммарная вертикальная реактивная сила фундамента (все гравитационные силы приложены к соответствующему центроиду с, с * * * — индивидуальная масса рассматриваемой системы), R ’ — суммарная тангенциальная реактивная сила фундамента. В Перейти к выпуску 267. Ттззззззззззззззззззти Л) \ РУБ. Д’ОР В Направьте ось y вертикально вниз с осью вращения кривошипа OA в качестве начала координат.
применим теорему к движению центра инерции системы масс в проекции на ось Y. м£= Чтобы… » Я сумма проекций всех внешних сил системы на ось Y: С / я Так… Мну = Пи + + ПБ-Р> Сила реакции основания MRc для решения проблемы- н Как известно, в этом выпуске M $ c = X McR / g к = I Мну=, -]- М, 7 классы + м $ б. (2) Рассмотрим механизм коленчатого вала во времени tt, когда кривошип ОА поворачивается на угол 9 = Вт / от нижнего вертикального положения. Центроид массы системы Q, Cb и координата C3 Y \ * yy показаны на рисунке. б)это легко увидеть Да. yy-ось y * = — y cos i0t = 2 cos / / ыы = = ОА, потому что у> Е — \ — Б, потому что ф-ф — £Са = Р потому что ж-ж — /, потому что ж-ж — £С3
Где отношение между углом w /и Phi равно、 Теорема синуса треугольника OAB: Син Фергюсон. 。 г。. х. 。 — = -. грех ф = — г sinОЯ = х Синт тут грех < в я / Где y =X. Тогда cosφ= K1 — = V \ — X9 sin3 y3 принимает вид: У3 = Р COS в — ф-г при cosφ= р потому что ж / — (- У1-* Формула В1 ->.* Разверните Sin2 в ряд/. Если X-нормальная дробь, отбросьте все члены ряда, содержащие X на уровне выше 2-го. То есть, | / l — > «sin *» * = 0-X ’ sin9 ^)7 ** 1-9sin9 Поэтому, если мы сосредоточимся на ВЗ = р потому что ДС-[-1 [[- J в Х1 sin9 9 которых J ZJCa; грех * у> ф = ^(я-cos2ш/) и у, мы получаем: = /-+ + р: потому что СПС-Ф \ Х потому что-я-БК. Вычислите 2-ю производную yl%yq,
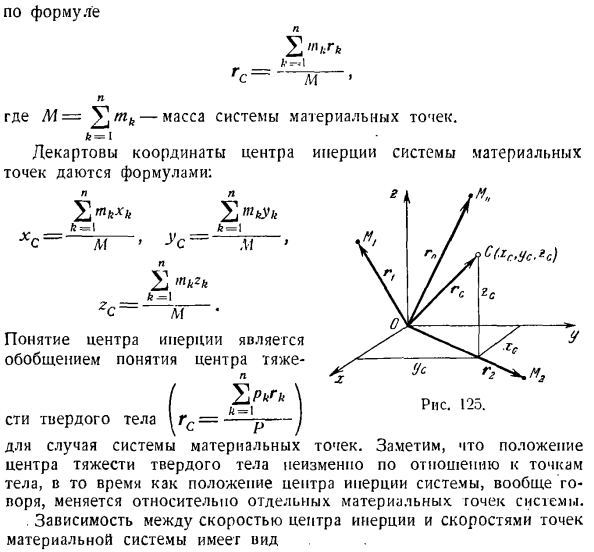
y3 относительно времени t. п, −0,= — Что ж, Пи =-rsh2(COS к / — п>.потому 2пк^). Теперь найдите Mus, подставив y, y в Формулу (2). Р п Atpc= -;» — r™ » cos W-ЛГш1 (ENS -).Cos2ю/)> Или MUS = — Γ ’<2рз) cos0 > γ -; −2).Р3 потому 2О)/ Дж. По формуле М Где M = V] ’7 * * — масса материальной точечной системы. Декартовы координаты центра инерции материальной системы задаются формулой: н к = 1 Л1 Мы= Один 2 ′ н ^ к Слева. Понятие центра инерции является обобщением понятия центра тяжести н (21 PIV к = \ Твердотельные СТИ
Для системы важных моментов. Обратите внимание, что положение центра тяжести твердого тела не изменяется относительно точек тела. С другой стороны, положение центра инерции системы изменяется, вообще говоря, относительно отдельных критических точек системы. 。Связь между скоростью центра инерции и скоростью точки материальной системы、 Мистер Им. Vvrjc / / * С (.ЗР, МК, СК)з * п Х г mkxk м
Введем формулу Mjfc 11 Формула (1)получена для определения вертикальной силы реакции фундамента. Р = р, — р, / > + РФР я (Пи-Г2Pa) косо* 2XPj потому что 2 <НФ]、 Фонд находится под наблюдением, и она создала свой закон. О Р т. Я ЕД / Л — В <И Г U2 Семьдесят семь С2 В С 7Z-В//////. ’’////)’ // л Это зависит от времени t. Требуемое давление конной повозки на противоположную сторону от обычной силы реакции R Выпуск 268.Вес P1 нагрузка A — это 2-й конечный вес P. it вибрирует на пружине, прикрепленной к неподвижному грузу B u. груз
B расположен на горизонтальной поверхности. Вертикальная сила реакции экспериментально определенной горизонтальной плоскости равна P = Pt-P. Если она равна 2C — / / cos si N, то она определяет закон колебаний нагрузки A. начальный момент A pa x n, сжатый из положения статического равновесия пружины, был выпущен без начальной скорости. Масса пружины игнорируется. Ответ рассматриваемая система состоит из 2-х масс I и B. представляет собой внешнюю силу. Pv-вес груза A, приложенного к центру тяжести C|, P» — вес груза I, приложенного к центру тяжести, и нет
гравитационной плоскости. Выберите точку отсчета на неподвижной вертикальной оси в положении статического равновесия для нагрузки L. Напишите теорему о движении центра инерции системы масс и проекции на ось Y. Мну = Е Е ’ V 2 с Выпуск 26 кя. В этом случае сумма проекций всех внешних сил системы Р= Так… МНУ = Р,+ Р * — Р- — Р Hcos ж / ’ тогда мну =-п, потому что искусство. Вычислите L / pc по формуле Mus = ^ ^ случай дампа К 1 ноября. Миссис = т \ г -}- Где Ух-это нужные номера-числитель, а J, где » 2 = = ОС2 является постоянным. Так… =(2) Подставляя знак Mus выражения (2)
в выражение (I), пах Ди! В: П — Ух = — / — / Коско /、& Г. е. п = — потому что МТ. (.*) Эго является дифференциальным уравнением движения груза А. из рассматриваемых условий исходными условиями для движения груза являются следующие: если T = 0 г \ = а, гг = 0.Когда я интегрирую дифференциальное уравнение (3), оно выглядит так: Да. После задания начального условия математическое ожидание/ = 0, j ’, = r = 0, Dx = 0, т. е. №、 После того, как вы снова интегрируете его, вы увидите следующее: — Г ’= tfcos с + Задание начальных условий t = 0, V \ = a для движения имеет вид: Итак, нагрузка а будет вибрировать в соответствии с законом Гц, НД й <ф Амплитуда колебаний равна-и круговые частоты колебаний равны. Задача 269.Планетарный
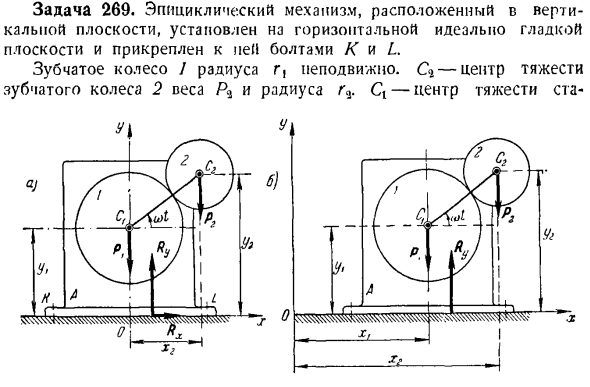
циркуляционный механизм, расположенный в вертикальной плоскости, установлен на идеально ровной горизонтальной плоскости и закреплен на горизонтальной плоскости болтами K и L. Радиус R шестерня 1, неподвижная. C * — центр тяжести груза A3 Gear 2, а радиус rQ — центр тяжести стадиона. Трубы А и колеса/, общий вес равен P. масса коленчатого вала [с]С9, который вращается с постоянной угловой скоростью o>, равна ignored. At в первый момент кривошип занял правильное горизонтальное положение
. 1) сила вертикального давления механизма на плоскость; 2)угловая скорость от вращения кривошипа, который при отсутствии Болта начинает пружинить на горизонтальной плоскости; 3)максимальная горизонтальная сила, действующая на болт; 4) перемещение центра тяжести Q станины механизма после резания P e ui e. материальная система состоит из 1 массы неподвижных колес с кроватью и 2 подвижных колес. Давайте объясним внешние силы этой системы. Суммарная вертикальная сила реакции плоскости, суммарная
касательная сила реакции от RX —вольтовой K и L. давайте сделаем ось y вертикальной через точку C, а ось*прямо вдоль горизонтальной плоскости. Опишите теорему о движении центра инерции системы в проекциях оси x и оси Y. £FTX, Который, / Муз -£/%. к = т к = 1 В этой задаче £БСЭ =£фи> = я,—Р * Так… Типа МХС = ГХ, ТУС = Ры-Пи-П «、 Иначе говоря RX = a 1xc, (1) Ры = туалет + Пи + п *(2) Чтобы определить мощность Rx и Ry, необходимо рассчитать Mls и Mus.
Расчет Атхк и ПДК осуществляется по формуле. Н П ССХ = 2 ТЗ * к и г = 2 т * р- В этом деле СОС = с — J-ял ’ 4 и LFS = / «$ 1 +(3) Где jcj и y {- координаты центра тяжести Q станины и неподвижного колеса Y механизма. xи y-координаты центра тяжести SL для подвижного колеса 2. Как видно из рисунка, X \ = 0, y \ = OQ-константа, x» = CyC cos cos =(r,-ri) cos wf (угол поворота кривошипа CiC4 равен
) грех мас. Время/относительно X \ y y, x. если вычислить производную 2-го порядка if y^, то получим: l’, = 0, y,= 0、 x * = — (r, r2) (0, J cos(оф.4= — (Гj-f-r. j) to4 Sin (от. Если ввести эти значения в выражение (3), то получится: Л С =-/ Л *(Р, — Ф-РЖ) о)’ 2 потому что о)^, (4) Afyc = — /»я + Ри) грех(5)
Подставляя (1) и (5) и (2) вместо (4), можно увидеть следующее: ГХ = — ^ ЧГ. ыы ^ aishl(6) Ры = РІ-р р * — J(с Р — Я-р)<о * грех «(7) Давление механизма на горизонтальную плоскость направлено в противоположную сторону от силы реакции, но становится равным ей. Ny = Pi />, — J(Г!- Гr2K деше/.Максимальное давление А; V в = п. -Я-а -; — ди джей + <а Минимальное давление А / г Ми » = — Г-(П + Г2) Вт * При отсутствии боли, механизм может начать подпрыгивать на горизонтальной поверхности. Это относится и к Rymin <^ Q. То есть в случае H, — R., — (rt 4 — * fi) l°2 Частота вращения Картера CjCj, на которую отскакивает механизм, должна удовлетворять
неравенству s > V » РЛ ^ Жг Горизонтальное давление, действующее на болт, противоположно (см. уравнение (6)) и далее ПХ — (РЖ я и) Ш’2 cosЫ. Максимальное давление равно п Лист—ы (Ри — | — Р2) (ОА. Предположим, что Болт сломался под действием силы Nx. Затем весь механизм начинает двигаться по идеально гладкой горизонтальной поверхности. Па рисунке б механизм нарисован в точке, где точка С1 смещена от оси y вправо. L-это функция времени t, так как станина механизма движется относительно оси X. Из рисунков, в данном
случае、 Xi = XV -) — CiCj, COS Uit = Xl (Г! РЖ потому ОТФ. н 2 М ’ <ВК S-М т. е. п п п п п С МК к 2 ′ мл д _ л^ Дж_ *- л. с.-м «-ч-Л1» — л / Здесь. Соотношение между ускорением центра инерции и ускорением точек материальной системы выражается в пропорциях Вт., = 21 ткщ S-М Так… Противоударный = ФН \ * я + ма — («’я-р-(н-ф-Р:) 0) 9 потому что апельсиновый сок /.(8) Движение центра инерции системы масс и теорема о проекции на ось Х、 Л < * С = Я Н Б = я Потому что никакая реактивная сила после резать Болт. И внешние / Я Мощность I, P. 2 и если Ry перпендикулярна оси jc, N} Fjv = l) и Один Аль \ ’ с =0.Подставляя значение/ Pl в уравнение (8) в это уравнение, получаем: (///п -///.>) х \ — г (р, с-J — Р2) Вт * потому что ж / = 0、 Иначе говоря * «=/r-p: C » + COS cot. (9 )) Это дифференциальное уравнение движения
центра тяжести станины Q механизма вдоль идеально гладкой горизонтальной плоскости без bolts. To интегрируя уравнение (0), необходимо знать начальные условия движения точки C. At в момент резания болта точка с находилась в естественном ПО и была неподвижной, поэтому начальные условия движения описываются в следующем виде: Если / = = 0 n:— — 0 и xx = 0. =(Ри + Р (0 грех + После замены начального условия движения^ = 0 и! Есть = (): D,= 0, то есть = / ^ ^Η (««Ф греха°> /. п Если вы снова интегрируете, вы увидите, что xx—yj—(r, — 4-cos wf 1 Дж~ ч * 2 — }- £==0, если jc1 = 0: = младший-К (р * -я-Р) 0-потому что В0- Таким образом, центр тяжести С, станина
механизма при отсутствии болтов, совершает гармонические колебания с амплитудой П&Т ^ + РЖ Круговая частота CICA равна скорости вращения кривошипа- Эта задача также может быть решена с помощью уравнений динамики переносимого motion. As известно, что поступательное движение системы происходит как абсолютное движение под действием всех внешних сил системы и силы инерции массы в их относительном движении. Мвтэ = с — J] J, к、 Кей! Где Feb-внешняя сила, а Jrk-сила инерции в относительном
движении. В проекции на ось декартовых координат имеются: МВО =£л » B — = 1 час-I Вт,=£+£ж к = 1 л = 1 = З + З И-и к = \ В этой задаче колесо 2, которое участвует в поступательном движении вместе с колесом U и станиной, совершает относительные вращательные движения вокруг колеса/и оси через станину перпендикулярно центру тяжести C1 и плоскости XY станины. Все внешние силы системы Pb, Pb, Rx, Ry были показаны (см. Рисунок C) Применить центробежную силу для относительного движения п Jrn = — — — * внешт.
От середины относительного движения О Образуя круг с радиусом C в центре Q, Q = Tj -} — r9, центростремительное ускорение wrn направлено от C2 к C, при этом центробежная инерционная сила относительного движения Jrn противоположна. По модулю./ начинать.= 5″•».= § ( ’ .+ ’ * ) «Л Инерции вращения в относительном движении огд = П — Кривошип вращается равномерно так, что он равен нулю. Мы применили дифференциальное уравнение поступательного движения материальной системы к проекции осей
x и Y. mkhe = 2, g’X — \ — V Jrixt из ft ^ — l £ 1 Мы получаем: Мхе = ГХ + Jrn с COS <КУП:= ры-Пы-п- ’ р Jrn греха Вт/. Хе = chius = Ил Jrn =% (р — п-р.2) В4、 Лига= /?х + | (р+ Р4) соѕ (0/, (10) Моя Г + 7 БСМ-г г*) грех со /. (11) Для скрепленного болтами механизма, колесо/и центр притяжения кровати Cj фикчированы. То есть X1 = j»i = 0, и дифференциальное уравнение принимает вид: ГХ + ПФ сі + р <т) COS и> / = 0,(12) Ry-Pi-Pi + 7 (n + r.) CO » 2 sinw/ = 0, (13) Таким образом, проекция вертикальной силы реакции самолета является р>
/ ?, = Р,+ Р2 — ^(Т+ Ж грех*.(14) Проекция на ось x горизонтальной реактивной силы Болта равна、 = + р г)В4 потому что ж *. (15 )) Условие отскока определяется из(14), Rvm \ n п Твердый. Ры Мин = + + + * * — Джей(Ри +(°с J> а О Здесь._ После разрезания болта колодки по формуле (10) определяют закон движения станины центра тяжести Q и механизма колеса, устанавливают Rx = 0. =(г, с-J — Р2) Тотт В4 потому что Я. e. To дойдем до Формулы (9). П、 Икс= \ 1 = 77777g. (G1 ″ 1-COS < Решение было получено выше. Проблема
270.Предыдущая задача решается в предположении, что эпициклический механизм прикреплен к упругой балке и изгибается на 1 см под действием силы, равной килограмму. Переходим к выпуску 270. При определении силы реакции пучка важным моментом для фокусировки на центре пучка считается эпициклический механизм».Если размер механизма меньше длины луча, то приближение является действительным». Определите закон вибрации центра тяжести С \станины механизма. Предположим, что в первый раз точка Q находится в положении статического равновесия, ее скорость равна величине r » 0, и она направлена вниз. Сопротивление массе и движению луча игнорируется. Кривошип
вращается по часовой стрелке с постоянной угловой скоростью(approximately. At в первый момент он занял правильное горизонтальное положение. Решение. Поясним внешнюю силу, приложенную к механизму: Px-это станина А и вес неподвижного колеса/, P. j-вес подвижного колеса 2,R-суммарная упругая сила балки. Положение статического равновесия центра тяжести Ci станины механизма, то есть Центра балки =(1) направьте ось y вниз. В этом случае теорема о движении центра инерции материальной точечной системы в проекции на ось y имеет вид、 M = р,+ р,+ р. р.(2) Mapip
и в точке C \движется вниз из положения статического равновесия, t, где CJ и C — located. In в этом случае кривошип C \ Cb поворачивается на угол 9 = co /(так как σ > постоянно). это легко увидеть. (3) В этот момент балка изгибается с Л>(=Лст-J-J/T, поэтому проекция силы упругости балки РВ =-cby == — ’ (АСТ + в). (4 )) Подставляя эту формулу Rv в Формулу(2), и считая, что из Формулы (I) она будет Pi — (- P * — = 0: / Да= — сухо. (5) Значение Afpc определяется по формуле LGrc = X, YL*.в этом случае Используя формулу(3), можно увидеть: Л(?С
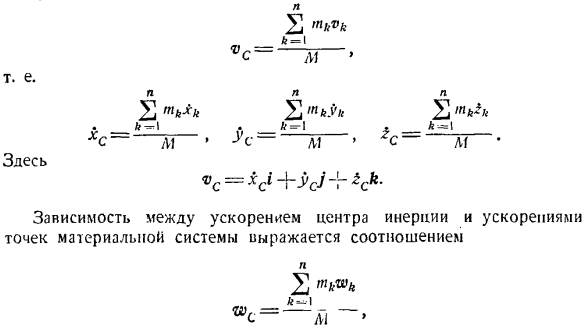
= с — J(р + р) ш <грех <из.(6) Подставляя значение Myc из Формулы (5) в формулу (6), получаем: =(Ри + РЗ)(0 * грех• Это дифференциальное уравнение вынужденных колебаний центроида с, лежащего в основе механизма. После введения обозначения Иначе говоря п п п п п 2, НК * н 2 ’»х 2″«.. = я_ В Л1 «> с-м » ^ с-ИИ• Здесь. wc ^ xci + ycj + zck. Решение задачи, в которой необходимо определить уравнения траектории движения центра инерции, должно осуществляться в следующем порядке: 1) Выберите систему координат. 2) Запишите координаты центроида каждой массы системы и выразите их как функцию времени. (О » — В*=«!> *(О «*а = Х * (0 » ™е л = …«л»; 3) определить
координаты искомого центра инерции материальной точечной системы по формуле: п п п п п 2 МК * к 2 2 ′» к2 * б = \ _ _ //• * я _ к = 1 XC M’US; \ 1 9 2 C M> Уравнение принимает вид p, — J — = h sinw/. (7 )) Общее решение дифференциального уравнения(7) выглядит следующим образом: — U1 = = UUDI + — V1 часто> Где _u1one-общее решение соответствующего однородного уравнения, а cast-частное решение уравнения(7).Решение y {one определяется из дифференциального уравнения jf, kLyx = 0.Вид характеристического уравнения равен r4 = 0.Корпус характеристического уравнения равен r, 2-интегральные константы.
При нахождении конкретного решения необходимо различать 2 варианта. а) если нет резонанса(co z / z / g), Б) если есть резонанс(co = k). Рассмотрим вариант а): для σ>Φ/ r конкретное решение найдено в виде частоты yx = ^ sin w / 4-B cosw/.Где A и B-постоянные коэффициенты, которые должны быть определены позже. Подставляя в ухо часть дифференциального уравнения (7), получаем: — АУ> * грех со / — кукиш * в COS со / — Ф-АКЛ грех со / Bfc1 в COS со / = ч греха со /. если уравнять левый и правый коэффициенты уравнения sinw/ и cosw / соответственно, то получится: A (L3-ω)= / 2, B (L2-CO2)=
0; Для Φk,-и H = 0, то есть конкретное решение Он в форме. Г \части-грех » Л(10) Подставляя значения yioia и _y1chast в формулы (9) и (10) в общее решение(8), получаем: Г \ = г 1 ояне +часто= 0 / потому что КТ-КТ Ф Грех + Грех тттт. (11) Чтобы определить интегральную постоянную, необходимо записать начальные условия движения точки Cj. Рассматриваемое условие указывает на то, что в первый раз точка Q находилась в положении статического равновесия, а скорость ce(величина, равная vn) была направлена вниз, то есть£= 0, y = 0 и = m » 0. Если вы зададите начальное условие = 0 в (11), то увидите, что оно равно yi = Di = Q.
Для определения он дифференцируется относительно времени γ1, как определено в уравнении (11). С ’ \ = — Д ^ к греху Дик КТ, потому что КТ-J-к, _ J не потому что МТ. Если присвоить J) начальному условию t = 0,= vQt, то получим: Здесь решение дифференциального уравнения вынужденной вибрации центра тяжести Cj станины механизма принимает вид отсутствия резонанса. ГУ «КТ + грех»> /、 Куда? Рассмотрим вариант Б): если существует m = k, то есть явление резонанса, то конкретное решение получается в следующем виде:>
1 часть = At sin w / — {- Bt cos cos to / — Лш9 / Sin A) T-2 W Sin U) T — # 9 / COS to / — f—4 £ 9 / sin to / — f- ВФС потому что тот = з грех /. если уравнять левый и правый коэффициенты уравнений sin и cosw / соответственно, то получится следующее (напомним, что вы использовали резонанс σ=£): — 2ч(п = з, 2 / З = О、 Итак, 4 = 0 и= = — / / / 2co, то есть форма частного решения равна -U1h. st = — frtCO&ut(12) Если вы присваиваете значение y1oda и y из выражения (8) (9) и (12) во многих случаях, вы можете увидеть следующее: = У \ одеа + У1 Хея-потому что жир + Д * грех ударить-потому что ж . (1 3) Если начальное условие движения, то есть t = 0 y1 = 0, то получим Z) i = 0. Чтобы определить D4, выделим его относительно времени y, которое
описывается формулой (13). Л л Ух = — Djto sinw^ -} — Д / О косо-Т ут греха г) 1!Начальные условия движения t = 0, j>! = v0, есть следующие: Около 1 1 I M Теперь дифференциальное решение урапипии вынужденных колебаний С-образного центра тяжести механизма при резонансе、 — V » = (•»I»£) ^ n » * — A t Cos ом/、 Где h = = 7j-t-5 (f i ^ a) вынужденная переменная амплитуда Л Колебание точки C \равно a=, y-t и возрастает прямо пропорционально времени. Эта задача, как и предыдущая, может быть решена с помощью переносных уравнений динамики поступательного движения. Колесо 2 участвует в поступательном движении вместе с центром тяжести Q станины,
а колесо 2 совершает относительные вращательные движения, перпендикулярные плоскости симметрии механизма, вокруг оси через центр тяжести C \колеса и центр тяжести C \станины. Все внешние силы: после рисования Pb Pb R (см. Рисунок B) добавьте центробежную инерционную силу к относительному движению Jrn== -. — РВ.«Потому что точка C <>описывается в относительном движении Центр-C, радиус-r, окружность-j-это центростремительное ускорение C. поскольку оно направлено от 2 до Ct, центробежная инерционная сила относительного движения Jrn противоположна. По модулю: R. P, h Jrn = — г п> м = grCi-г » к- включите питание
интерфейса!!。Ui в относительном движении — — — — ’wr. It это то же самое, что и пуля, потому что кривошипы вращаются равномерно. применение дифференциальных уравнений поступательного движения материальной системы в проекции на ось Y: Н. Н. Н. X Fly+ 2 jerky K = 1 k = I Мы получаем; ПДВ = п — п— п * — р-и — й-грех стеклоподъемников(14) Присвоение уравнению(14) Также из Формулы (4) Формулы Rv = — c (ACT-J-Vi) можно видеть: = P. + P> — ω,+ + J (Γ,+ r Jω3sinЛΛ(15) о б Исходя из Формулы (1), Если P * — cDst = 0、 Получим дифференциальное уравнение(7) в виде y, — f- / r2uh =
h sin N, где** * * а?= y (r, — f-g.2) Дельта-интегрирование OL ’1〜г’ 2 1 ′ ый В первом варианте решения этой задачи было выполнено международное уравнение (7). Задачи 269 и 270 решались двумя способами: применяя теорему к движению инерционного центра масс системы и используя уравнения динамики клеточного поступательного движения. Степень сложности решения задачи этими способами следует считать практически равной. 3 при сохранении скорости движения центра инерции системы масс. Внешний основной вектор н Если сила системы равна нулю (Ve= V =
0), то скорость центра равна Ко мне. Кроме того, размер и направление системы III остаются прежними(ty?- Постоянно), то есть инерционный центр системы материальных точек движется равномерно и прямолинейно или находится в покое. Если скорость центра инерции равна нулю в определенных случаях: 1> c = 0(например, это происходит, когда система неподвижна в начальный момент), то независимо от оставшегося состояния центра инерции критическая точка системы может быть перемещена, кроме того,
сумма масс точек на векторе инерции равна нулю.、 н Ноль, то есть 2 мкбрк = Q !<= \ н Аналогично, в проекции на ось x, если ^-0 «то-по * k = I н Это хорошая идея. Если xc = 0 в конкретном случае, то^ rnk ^ xh = 0. k = I Задача 271.Может ли человек ходить по идеально гладкой горизонтальной поверхности? Решение. Внешняя сила, приложенная к человеку, — это его вес P и общая вертикальная сила реакции R Земли.
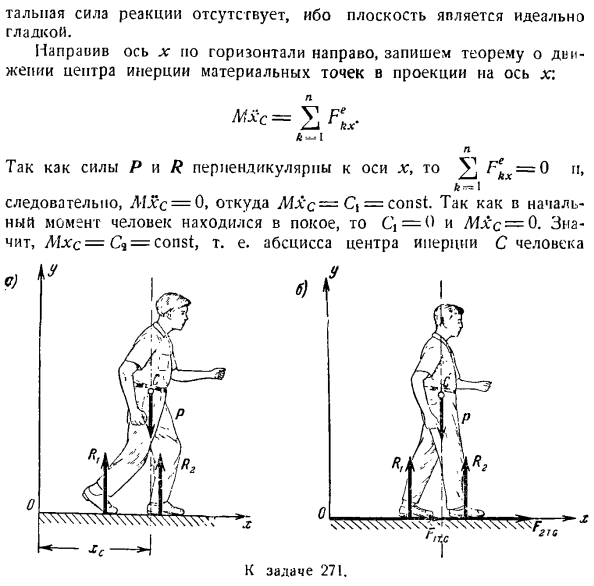
Плоскость совершенно гладкая, поэтому нет таллиевой реактивной силы. направьте ось x горизонтально вправо и запишите теорему о непрямом инерционном движении материальной точки в проекции на ось X. л А-Я л Поскольку силы P и R перпендикулярны оси x,^ = 0 n Я В результате A1xc = 0, из которого M&c-C » = const. At в первый раз человек отдыхал, так что это C,= 0, Mx = 0. Как бы то ни было, человек не может ходить по гладкой горизонтальной поверхности. Еще, например, если вы поднимете левую ногу и попытаетесь поставить ее впереди, то правая нога будет двигаться сзади, и абсцисса центра инерции xc не изменится. Человек может
двигаться по гладкой горизонтальной поверхности и бросать предметы вперед(или назад).Затем он начинает двигаться в противоположном направлении, то есть назад(или вперед). Если человек, стоящий на гладкой горизонтальной поверхности, хочет прыгнуть, он может это сделать it. In дело в том, что теорема о движении центра инерции материальной точечной системы в проекции на ось y выглядит следующим образом: Мельница= /? — / > В этом случае вы можете видеть, что xc> yy, zc является функцией премии. То есть полученная формула будет параметрическим уравнением движения центра инерции. 4) чтобы найти явное уравнение локуса центра масс точечной системы, нужно исключить
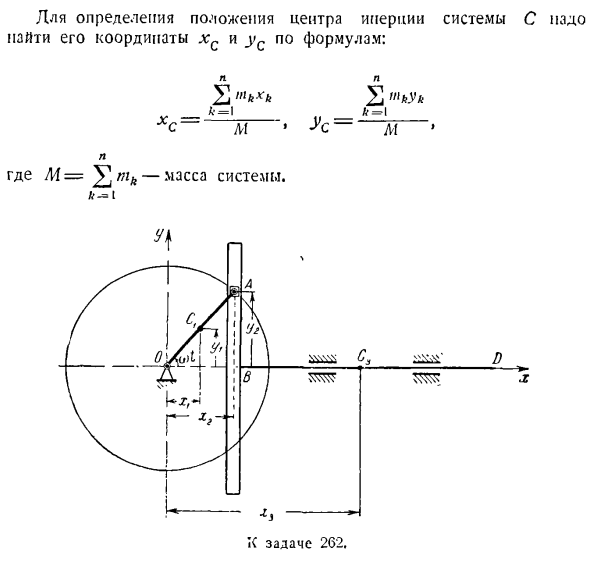
время из последнего уравнения. Проблема 262.To определите уравнение траектории движения центра инерции коромысла механизма, показанное на рисунке, если масса кривошипа ОА равна яме, то масса породы коромысла А равна А, а масса коромысла и стержня БД равна Р3.Кривошип, вращающийся с постоянной угловой скоростью ω, считается пятнистым однородным стержнем и считается каменной точечной массой. Центр тяжести кулисы и стержня находится в точке C; b, OA = AFL = 1 в первый момент скала кулисы A занимала крайнее правое положение. Решение. Выберите ось декартовых координат, показанную на рисунке. От него расположение рычажного механизма соответствует времени t. так
как кривошип вращается равномерно, то каков угол его поворота? Он равен Т = П1. При отталкивании от Земли из-за деформации мышц получается R ^> P. То есть, центр инерции человека Перемешайте по вертикали. В этом случае сила трения скользящей ноги прикладывается к упомянутой внешней силе от подошвы человека на земле и направляется в направлении движения, так что человек может ходить по негладкой горизонтальной поверхности(см. Рисунок Б). в этом случае вы получаете Проблема 272.In наклонная плоскость KL усеченной четырехугольной колонны DEKL, вес load =
10 кг нагрузки.4 опускается и вес Рв = 6 кг невесомой нерастягиваемой нити перемещается под действием нагрузки. Если нагрузка A движется вниз по наклонной плоскости KL на 1 м, то мы находим, что призма DEKL с весом P = 20 кг движется по идеально гладкой горизонтали surface. At в первый момент система была остановлена. Решение. Обозначим все внешние силы, приложенные к материальной системе, состоящей из призмы и 2-х Весов. И внешние силы: Р-вес призмы, РА-нагрузка веса \ Pfi-это вес груза B, а P-полная вертикальная сила реакции горизонтальной плоскости.
Горизонтальная плоскость совершенно ровна, поэтому никакая сползая сила трением между призмой DEKL и горизонтальной поверхностью. напишем теорему о движении центра инерции материальной точечной системы в проекции этого шершня, причем ось Х направлена горизонтально вправо м * ы =£н、- k = I н Потому что все внешние силы перпендикулярны оси x、 Я Так Что Mxc = 0. Mxc = Ci. Во-первых, система была stopped. So, Cj = 0 и Mxc = 0. ССХ = Съ То есть абсцисса центра инерции системы остается постоянной, независимо от движения отдельных масс, входящих в систему. Из определения центра инерции материальной точечной системы、
л ССХ = 2 tnuxk-Н = [ Координаты материальной точки системы, соответствующие моменту начала движения, указываются в индексе I, а координаты, соответствующие моменту окончания движения, — в индексе 2.И затем… л для T = i \ MxQ = Y ^ fnhXlh、 К-И-Л т =(я типа МХС = £ / HkXik. Один Если вычесть первую корреспонденцию из 2-ой корреспонденции, то она выглядит так: К k = I значение < xik-x \ b = B B B B B B B B B B B C < если абсцисса инерции постоянной xc равна некоторому периоду материальной точечной
системы, то происходит смещение точки материальной системы, и сумма произведений массы точек на величину л Ноль смещения оси l равен нулю:^ mk \ xk = 0. к-мне Напишите к этой задаче: mAkxA — J-vl ^ Xq-rtAx = 0、 Где&x-желаемое горизонтальное перемещение призмы. Если вы выражаете массы тела через дьявола, то: 10 (Da—J-1.Cos60e) −6(Д-V+ 1)-20дх = 0. (При решении таких задач часто совершаются массовые ошибки. Проекция вводимой массы и движение системы регистрируются не для абсолютных движений, а для относительных движений.
Чтобы определить положение центра инерции системы С, найдите координаты xc и усы по формуле: Н. Н. Н. 2 ″ ИК * к 2 _ А = Л _ УГ-м ’»нас-м’ н Где Л1= 2 МК-масса системы. Поскольку рассматриваемая система состоит из 3 корпусов за кулисами с кривошипами OA, Stone A и BD bars、 C wi1-f- //(2 + ’ С/’!- Да.2+» / и3•*’ Здесь индекс 1 соответствует кривошипу, индекс 2-камню а, а индекс 3-крыльям с barbells. As вы можете видеть из диаграммы: Х \ = 2 соѕ W (В, Г,= -!- Син ж(、 Х)= / Что ж/, У2 = я wty грех Х3 = Х2 — | — 1GC3 = / потому что(о / — (- /=/(л -] — cosш/), _ У3 = 0. Подставляя символы xi yy, y3 и Формулу (1), и выражая массу звена механизма через его веса,
получаем: Потому что пи (О/ -е ПиДжей Cositit4-pfv-максимальное прямое напряжение (я ведь немного) = Р,/, л + 2Pa•ч 2P3 ~~ Пи + па + п * «т» *(р | — ф » п. ч. Р3) потому что т0 ″ МК РТ + Р2 + ПТ 1 {ФВ + Р2 + РЗ} грех Найти уравнение траектории движения центра инерции Необходимо исключить время из этих уравнений движения. если вы решите оба уравнения для cos cot и sin wt\, а затем возведете их в квадрат и сложите, вы получите: / _ _ / г Г л> я + ПФ \ — Р>), — ВК = 1. 1 Г (RN-2P、)/ [2 (Пи 2 (P,+ Pe + P.) J L2 (Pl + Pe + Pe)| Поэтому локусом
центра инерции коромысла механизма является эллипс полуоси. н-ч-(ч * + 2П)/ 2(П4 + п+ пп 2(п | о + Пн + па Центр эллипса находится на оси x и в стороне от начала координат O. П И Справа вдалеке -^—.-. ’Второй’ я ’ я ’ 3 1 я 2°.Теорема о движении центра инерции материальной точечной системы. Центр инерции материальной точечной системы движется как материальная точка.
Его масса равна массе материальной системы, и все внешние силы, действующие на систему, приложены. КТМ =±1 ″ Форма же теоремы, записанной в проекции на ось декартовых координат, выглядит следующим образом: у * с =£ПХ, то WS =£Н、 Л-Г Я… * 1-я Движение центра инерции материальной точечной системы зависит от внешнего force. It подключается к этой системе. Внутренние силы, не включенные непосредственно в описание теоремы
Смотрите также:
Предмет теоретическая механика

