Теорема Кёнигса

Оглавление:

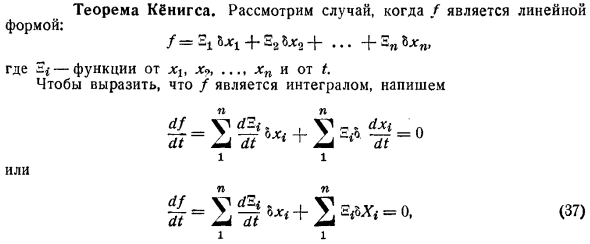
Теорема Кёнигса

Рассмотрим случай, когда f линейная форма. = Х1 4 С2 + … 4 2nLxn. Где 2 х,…функции xn и t. чтобы показать, что f является интегралом Или 37 = S + S E, и = 1 1 37 вы можете написать: Уравнение 38 легко приводит к доказательству элегантной теоремы Кенига Kcenigs, Comptes, rendus, 1895 12. Линейная дифференциальная форма является предметом многочисленных исследований, и особенно исследования Пфаффа пытались свести их к некоторым каноническим системам Darboux, Bulletin des Sciences mathdmadiques, vol. ХVII, 1882, стр. 16 Gupea, лимоны сюр Ла provte дю pufaf, Париж, 1922. Работа Э. Картана посвящена тому же формату.

Фактически доказано, что каждая линейная производная форма может быть сведена к одному из следующих 2 типов: р и Y1 4 R2 и Э2+ 4 г УР г Ля oy1 + r2 oy2… Рост Н Б Здесь переменные y, yt,…г, злт… zp не зависит от каждого other. To чтобы получить эти упрощенные формы, необходимо интегрировать некоторые дифференциальные уравнения, ссылаясь на статью Дарбу для ее изучения.

Кривая, соединяющая две неподвижные точки А и В, и переход от одной из этих кривых к другой бесконечно близки, изменение действия равно нулю, и если она проходит через одну и ту же точку, то становится одинаковой. Людмила Фирмаль

Здесь мы применяем процесс редукции к форме, где t считается постоянной, например 2 Предположим, что у вас есть формат A , который включает переменную 4 1. Бывают случаи, когда 2П 4 1 меньше, чем л, то y, УГ… …Чтобы прикрепить к 1… 2р переменной ттж,…. В Uq, количество q = n 2p 1, Вы можете использовать количество y, r и u в качестве новых переменных. Тогда в этих новых переменных система дифференциальных уравнений принимает вид: ды дурь dzv ДЗ ДЗП = ТП = ЗТ = = з Где, Yit …. Гг, ЗБ…. ЗП, УБ… Uq это переменная y, yx,… …Это функция злт…, Ио и Т.

Условие 38, здесь 2 является ay Sy, поэтому оно выглядит так: Поставь 40 41. Тогда мы получаем о 7 + Zi5yi Р Ози = о 42 поскольку это равенство должно применяться к любому b dN dN Zi = Wi Yi + dFi Тогда Г =. get n = r, g e n. я есть. Таким образом, вид системы дифференциальных уравнений 39 имеет вид ды ДТ + ДЗ Держзовнишинформ Т дх ДТ ды = Б 2,.. Р, 43 ды дх ДТ Дуди дзи ч 44 дю ор категории КР 45 Таким образом, мы достигли канонической системы наряду с системой уравнений 44 и 45 43. Если вы приведете f вместо формы A к форме B , она будет работать точно так же, достигая условия.

Как уже упоминалось выше 2 р р + 2 р б = Ви Так что H удовлетворяет уравнению здесь Другими словами, H 1 я однородная функция того же порядка относительно Z. Тогда система дифференциальных уравнений превращается в систему уравнений Дми ду dZj ду ДТ дзи ДТ дю Вместе с уравнением дю ДТ 46 47 если нечетно и f произвольная целочисленная линейность относительно переменной, то легко доказать, что она имеет вид A .Далее, n = 2p 1, наоборот, если n четно, то это будет в виде B , а n = 2p. So, в общем случае не существует дополнительной системы уравнений 45 или 47 и, в зависимости от n, сводит уравнение к канонической форме, с уравнением 44 или без него.

Поэтому, если к поступательной скорости добавляется поступательное переносное и вращательное относительное движение твердого тела, которое перпендикулярно относительной оси вращения, эквивалентное абсолютное движение параллельно относительной оси вращения. Людмила Фирмаль

Если n нечетно, то Интеграл 2 s после преобразования в стандарт равен Я 2П + Л К = П Г е БК г K = 1 В частности, если S не зависит от переменной t, то это будет: 2Д + 1р Г = Ай 1 1 Или запомнить его ДХ = Xtdt, дык = + ДТ ды Х + З ДТ Семитизм. 48 Один Таким образом, сумма сводится к основной функции N. H является интегралом, как мы знаем, тогда независимым от времени.. Это когда X или S не зависят от времени. Заметим, что во всех случаях формула 44 сводится к квадратуре.

Приложение. Задача Бруна (Brun)	Теорема Пуассона
Свойства интегралов. Интегральные инварианты. Интегралы	Интегральные инварианты

Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.