Оглавление:
Теорема Кориолиса о сложении ускорений
Теорема. Абсолютное ускорение 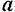 точки при произвольном переносном движении равно геометрической сумме трех ускорений-, переносного
точки при произвольном переносном движении равно геометрической сумме трех ускорений-, переносного 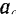 относительного
относительного 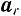 , и некоторого добавочного ускорения
, и некоторого добавочного ускорения 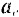 называемого повороты и или кориолисовым ускорением:
называемого повороты и или кориолисовым ускорением:
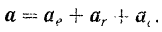
Доказательство.
Пусть точка 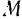 движется относительно подвижной системы
движется относительно подвижной системы 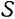 , которая сама произвольным образом перемещается относительно неподвижной системы
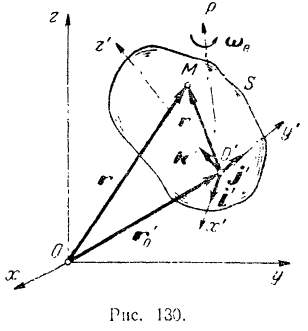
, которая сама произвольным образом перемещается относительно неподвижной системы 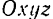 (рис. 130). Как было сказано ранее (§ 54), любое движение свободного твердого тела можно считать составленным из двух движений: поступательного движения со скоростью произвольно выбранной точки тела (полюса)
(рис. 130). Как было сказано ранее (§ 54), любое движение свободного твердого тела можно считать составленным из двух движений: поступательного движения со скоростью произвольно выбранной точки тела (полюса) 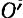 и вращательного движения вокруг мгновенной оси
и вращательного движения вокруг мгновенной оси 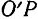 , проходящей через выбранный полюс (рис. 130).
, проходящей через выбранный полюс (рис. 130).
Обозначим мгновенную угловую скорость вращения подвижной системы 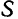 через
через 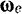 и будем называть ее переносной угловой скоростью.
и будем называть ее переносной угловой скоростью.
Примем полюс 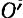 за начало подвижной системы координатных осей
за начало подвижной системы координатных осей 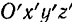 , неизменно связанных с подвижной системой
, неизменно связанных с подвижной системой 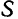 , и отложим на ее осях единичные векторы
, и отложим на ее осях единичные векторы 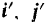 и
и 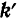 . Координаты точки
. Координаты точки 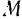 относительно подвижной системы координат обозначим через
относительно подвижной системы координат обозначим через 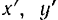 и
и 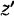 . Положение точки
. Положение точки 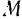 относительно неподвижной системы отсчета определяется радиусом-вектором
относительно неподвижной системы отсчета определяется радиусом-вектором 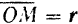 , положение полюса
, положение полюса 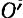 относительно той же системы отсчета— радиусом-вектором
относительно той же системы отсчета— радиусом-вектором 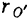 и положение точки
и положение точки 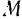 относительно подвижной системы отсчета — радиусом-вектором
относительно подвижной системы отсчета — радиусом-вектором 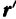 .
.
Как было установлено в предыдущем параграфе:
переносная скорость точки
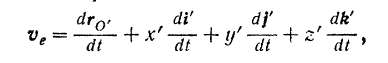
относительная скорость точки
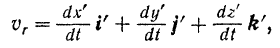
абсолютная скорость точки
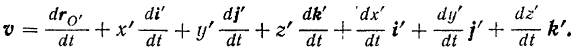
Найдем переносное 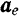 , относительное
, относительное 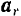 и абсолютное
и абсолютное 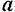 ускорения точки как производные но времени от соответствующих скоростей.
ускорения точки как производные но времени от соответствующих скоростей.
При определении переносного ускорения 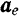 точки
точки 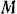 надо остановить мысленно ее относительное движение и считать координаты
надо остановить мысленно ее относительное движение и считать координаты 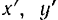 и
и 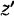 точки относительно подвижной системы постоянными величинами. Тогда, дифференцируя равенство (I), будем иметь:
точки относительно подвижной системы постоянными величинами. Тогда, дифференцируя равенство (I), будем иметь:
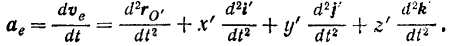
При определении относительного ускорения 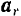 точки
точки 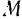 надо, наоборот, остановить мысленно ее переносное движение и считать орты
надо, наоборот, остановить мысленно ее переносное движение и считать орты 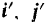 и
и 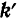 постоянными векторами. Дифференцируя равенство (II), будем иметь:
постоянными векторами. Дифференцируя равенство (II), будем иметь:
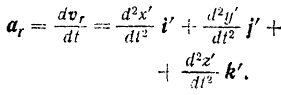
При определении же абсолютного 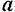 ускорения точки
ускорения точки 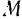 в случае произвольного движения подвижной системы координат орты
в случае произвольного движения подвижной системы координат орты 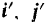 и
и 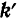 так же, как и координаты точки
так же, как и координаты точки 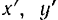 и
и 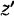 , надо считать переменными величинами. В этом случае, дифференцируя равенство (III), будем иметь:
, надо считать переменными величинами. В этом случае, дифференцируя равенство (III), будем иметь:
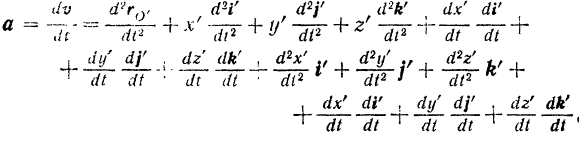
Или, соответственно группируя члены, стоящие в правой части последнего равенства, получим:
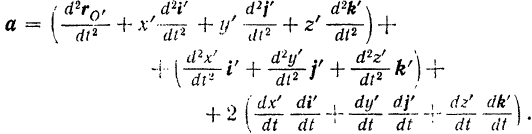
Первые два выражения, стоящие в правой части равенства (VI) и заключенные нами в скобки, представляют собой правые части равенств (IV) и (V), т. е. переносное 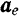 , и относительное
, и относительное 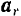 ускорения точки.
ускорения точки.
Найдем значение выражения, заключенного в последние скобки правой части равенства (VI).
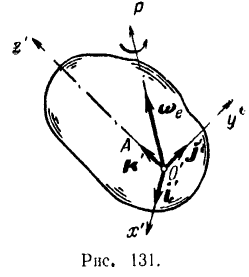
Отложим в соответствии с установленным ранее правилом (§ 54) на мгновенной оси 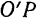 вращения подвижной системы
вращения подвижной системы 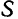 отсчета переносную угловую скорость
отсчета переносную угловую скорость 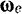 (рис. 131) этой системы. Вектор
(рис. 131) этой системы. Вектор 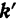 можно рассматривать как радиус-вектор точки
можно рассматривать как радиус-вектор точки 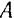 относительно полюса
относительно полюса 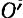 , и поэтому вектор скорости этой точки
, и поэтому вектор скорости этой точки
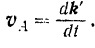
При вращении подвижной системы 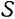 вокруг мгновенной оси
вокруг мгновенной оси 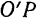 скорость
скорость 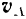 какой-либо точки
какой-либо точки 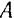 , неизменно связанной с этой системой, определяется, как известно 54), по формуле (91)
, неизменно связанной с этой системой, определяется, как известно 54), по формуле (91)
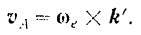
Из сравнения равенств (VII) и (VIII) находим, что
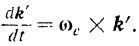
Рассуждая аналогично, будем иметь:
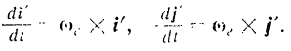
Следовательно,
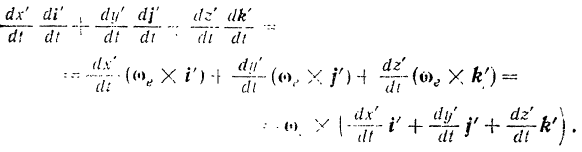
Из равенства (II) следует, что
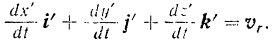
Таким образом, выражение
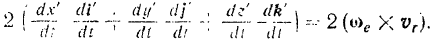
Заменяя все выражения, стоящие в правой части равенства (VI) и заключенные в скобки, найденными их значениями (IV), (V) и (IX), будем иметь:
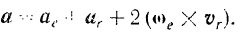
Последний член данного равенства, равный
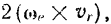
носит название ускорение Кориолиса. Обозначая его через 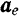 , окончательно получаем:
, окончательно получаем:
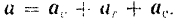
Теорема доказана.
Если подвижная система отсчета движется поступательно, то очевидно, что 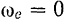 , и поэтому кориолисова ускорения
, и поэтому кориолисова ускорения 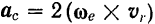 точка иметь не будет.
точка иметь не будет.
В этом случае
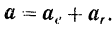
При поступательном переносном движении абсолютное 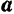 ускорение точки равно геометрической сумме двух ее ускорений, переносного
ускорение точки равно геометрической сумме двух ее ускорений, переносного 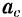 и относительного
и относительного 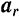 .
.
Важно заметить, что в то время как абсолютная скорость точки равна геометрической сумме ее переносной и относительной скоростей во всех случаях (при любом характере движения подвижной системы отсчета), абсолютное ускорение точки равно геометрической сумме ее переносного и относительного ускорении только в том случае, когда подвижная система отсчета движется поступательно.
Пример задачи:
Прямолинейная кулиса кривошнпно-кулненого механизма (рис. 132. а) приходного молота совершает возвратно-поступательное движение. Кулиса приводится в движение камнем (ползуном) 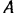 , соединенным с концом кривошипа
, соединенным с концом кривошипа  , длина которого
, длина которого 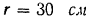 и который вращается равномерно с угловой скоростью
и который вращается равномерно с угловой скоростью 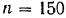 об/мин. При
об/мин. При 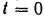 кулиса занимает низшее положение. Найти скорость и ускорение молота (кулисы) в момент
кулиса занимает низшее положение. Найти скорость и ускорение молота (кулисы) в момент 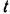 .
.
Решение:
Выразим угловую скорость кривошипа в радианах в секунду
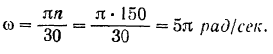
Будем отсчитывать угол поворота кривошипа от его низшего вертикального положения. Тогда при
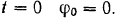
Следовательно, по формуле (88) угол поворота кривошипа
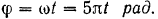
Абсолютная скорость точки 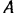 (центра шарнира, соединяющего кривошип с ползуном) равна по модулю
(центра шарнира, соединяющего кривошип с ползуном) равна по модулю
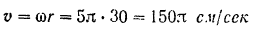
и направлена перпендикулярно к радиусу  кривошипа в сторону его вращения.
кривошипа в сторону его вращения.
С другой стороны, точку 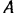 можно считать участвующей в двух движениях: относительном — горизонтальном движении ползуна вдоль подвижной направляющей (кулисы), и переносном — вместе с вертикальным поступательным движением кулисы.
можно считать участвующей в двух движениях: относительном — горизонтальном движении ползуна вдоль подвижной направляющей (кулисы), и переносном — вместе с вертикальным поступательным движением кулисы.
Строим параллелограмм (рис. 132,а), диагональю которого является известный по величине и по направлению вектор 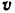 абсолютной скорости точки
абсолютной скорости точки 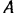 , а сторонами — известные только по направлению векторы относительной
, а сторонами — известные только по направлению векторы относительной 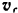 и переносной
и переносной 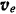 скоростей той же точки.
скоростей той же точки.
Из построенного параллелограмма (прямоугольника) находим скорость молота (кулисы), служащую для точки 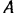 переносной скоростью:
переносной скоростью:
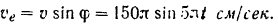
Так как кулиса совершает прямолинейное поступательное движение, то ее ускорение
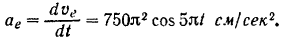
Ускорение кулисы можно было бы найти и другим путем. Так как кривошип вращается равномерно, то абсолютным ускорением точки  является ее центростремительное ускорение
является ее центростремительное ускорение
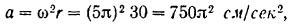
направленное по радиусу 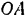 к центру
к центру  вращения кривошипа. Разложим это ускорение (рис. 132,6) по правилу параллелограмма на составляющие: переносное
вращения кривошипа. Разложим это ускорение (рис. 132,6) по правилу параллелограмма на составляющие: переносное 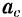 и относительное
и относительное 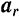 ускорения точки
ускорения точки 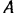 . Так как переносное и относительное движения — прямолинейные, то и ускорения точки
. Так как переносное и относительное движения — прямолинейные, то и ускорения точки 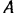 в этих движениях будут направлены по соответствующим прямым.
в этих движениях будут направлены по соответствующим прямым.
Из параллелограмма ускорений находим ускорение молота (кулисы), служащее для точки 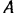 переносным ускорением:
переносным ускорением:
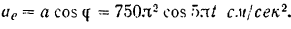
Пример задачи:
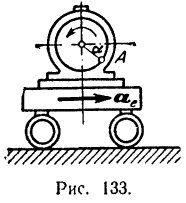
На тележке (рис. 133), движущейся с ускорением 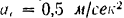 по горизонтальному пути вправо, установлен электромотор, ротор которого при пуске в ход вращается согласно уравнению
по горизонтальному пути вправо, установлен электромотор, ротор которого при пуске в ход вращается согласно уравнению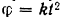 (
(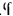 — в радианах,
— в радианах, 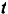 — в секундах). Коэффициент
— в секундах). Коэффициент 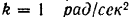 . Радиус ротора
. Радиус ротора 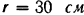 . Для момента
. Для момента 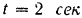 определить ускорение точки
определить ускорение точки 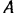 , лежащей на ободе ротора, если в этот момент точка
, лежащей на ободе ротора, если в этот момент точка 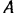 находится в положении, указанном на рисунке (угол
находится в положении, указанном на рисунке (угол 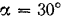 ).
).
Решение:
Точка 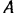 участвует в двух движениях: относительном—вращении вокруг оси ротора и переносном — поступательном движении вместе с тележкой. Так как переносное движение — поступательное, то абсолютное ускорение точки
участвует в двух движениях: относительном—вращении вокруг оси ротора и переносном — поступательном движении вместе с тележкой. Так как переносное движение — поступательное, то абсолютное ускорение точки 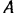 равно геометрической сумме относительного и переносного ускорений.
равно геометрической сумме относительного и переносного ускорений.
Находим угловую скорость и угловое ускорение относительною вращения ротора
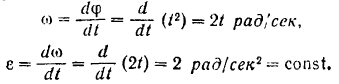
Для момента
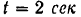
будем иметь:
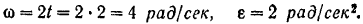
Так как ротор вращается неравномерно, то ускорение его точки 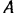 будет складываться из вращательного ускорения
будет складываться из вращательного ускорения 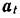 и центростремительного ускорения
и центростремительного ускорения 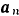 . Первое из них находим по формула (84)
. Первое из них находим по формула (84)
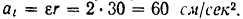
Так как угловое ускорение 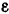 положительно, то ускорение
положительно, то ускорение 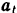 будет направлено по касательной к окружности ротора в точке
будет направлено по касательной к окружности ротора в точке  в сторону вращения.
в сторону вращения.
Центростремительное ускорение находим по формуле (85)
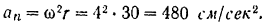
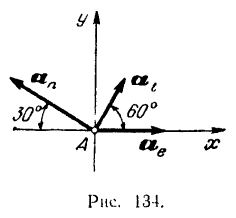
Полное относительное ускорение точки 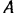
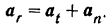
Абсолютное ускорение точки 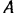 будет равно
будет равно
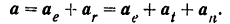
Ускорения 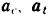 и
и 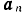 точки
точки 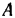 показаны на рис. 134. Так как проекция геометрической суммы векторов на любую неподвижную ось равна алгебраической сумме проекций на ту же ось составляющих векторов, то проведя через точку
показаны на рис. 134. Так как проекция геометрической суммы векторов на любую неподвижную ось равна алгебраической сумме проекций на ту же ось составляющих векторов, то проведя через точку 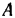 две взаимно перпендикулярные оси
две взаимно перпендикулярные оси 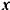 и
и 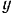 (как показано на рис. 134) и проектируя на них векторы составляющих ускорений, получим:
(как показано на рис. 134) и проектируя на них векторы составляющих ускорений, получим:
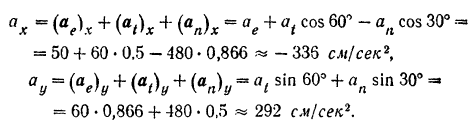
Модуль абсолютного ускорения точки 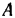 равен
равен
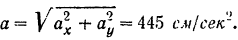
Направление абсолютного ускорения точки 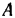 определив направляющие косинусы вектора
определив направляющие косинусы вектора 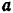 :
:
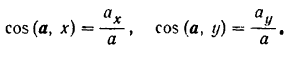
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

