Оглавление:
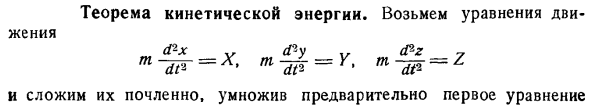





Теорема кинетической энергии
- Возьмите уравнение движения и добавьте его для каждого члена. Сначала умножьте первое уравнение на dx, второе на dy, а третье на dz. Возьми t dx 4 Jr dy + S DZ = x dx + Y dy + z dz. Квадрат скорости Это уравнение можно записать в виде: д Xdx г ды + Здз. 1 Произведение полумассы 4 2 на квадратную скорость называется кинетической энергией. Таким образом, предыдущее уравнение может быть выражено как: Разница в кинетической энергии за период dt равна основной работе равнодействующих сил, действующих на точки за тот же период.
Действительно, справа Х DX г ды 4 З ДЗ. Уравнение представляет собой основную работу силы X, Y, Z против действительных перемещений dx, dy, dz и создает точку за определенный промежуток времени dt. Результирующая работа X, Y, Z, как вы видели параграф 77, может быть заменена суммой работы отдельных сил, приложенных к точке движения. Уравнение 1 непосредственно следует из первого естественного уравнения движения. получить уравнение в v умножить и заменить на ds Здесь правая сторона равна основной работе силы F относительно перемещения ds. Если проинтегрировать уравнение 1 с момента t, то скорость времени 0 выражается в r 0, тогда: Т 2 МВО п = J Xdx + Y dy + Zdz, 2 t.
Оба конца скользят без трения по двум одинаковым соприкасающимся внешним образом окружностям, центры которых лежат на одной высоте. Людмила Фирмаль
Представляет собой следующую теорему В оригинале вместо названия кинетическая энергия автор использует устаревшее и ныне устаревшее название живая сила, величину to2 автор называет живой силой. Примечание, пер. Изменение кинетической энергии точки На любом временном интервале равно полной работе силы, приложенной к точке за тот же период. С точки зрения оценки всей работы необходимо выделить 3 случая, как указано в IV главе. 1. в наиболее распространенном случае, когда X, Y, Z зависит от x, y, 2, x , y , Y, t для вычисления суммарной работы необходимо знать координату x, y, z представления функции t, то есть нужно знать движение. 2.
Если X, Y, Z зависят только от x, y, z, то для вычисления полной работы достаточно знать траекторию движения точки между позицией A0, занятой моментом моментом t, и позицией M, занятой моментом T. 3.Наконец, если результирующие X, Y и Z зависят только от положения движущейся точки и имеют силовую функцию U x, y, z , т. е. Xdx г ды з ДЗ = дл х, у, Z. Затем вы можете рассчитать общую работу, зная только позиции LG0 и M. In в этом случае теорема о кинетической энергии приводит к первому интегралу.
Действительно, сделайте интеграцию. В правой части уравнения 2 2 2 МВ МВ г 2 2 = 1 Х, У, 2 у х0.У0, 2О Или U х, у Где A обозначает произвольную константу U x0, 0, 20 это Постоянная называется постоянной кинетической энергией. Согласно этому уравнению, каждый раз, когда функция U принимает Предыдущее значение, скорость движущейся точки будет такой же, как и раньше. Если U однозначная функция x, y и z, то можно сказать, что скорость движущейся точки принимает одинаковое значение при возвращении на один и тот же уровень поверхности U x, y, z = const.
- U x, y, z = arctg если функция U принимает более одного значения, например j, когда точка возвращается на одну и ту же ровную поверхность. Функция U x, y, z , и в результате полная работа принимает другое значение вдоль пути см. пункт 82. Образцы. 1. Рассмотрим тяжелую точку, которая совершенно свободно движется через пустоту.
Если ось Oz вертикально вверх, то сила, приложенная к точке, является только весом, поэтому ее проекция равна X = 0, Y = 0, Z = mg, и уравнение получается теоремой о кинетической энергии д ДЗ Правая сторона это идеальный дифференциал, который, как указывалось много раз, указывает на то, что есть функция, которая должна быть в весе. Когда вы интегрируете П2 г 2 г г г ox 2 = 2 —ГЗ + а. Уравнение показывает, что скорость всегда принимает одно и то же число, когда точки находятся на одной высоте, то есть когда они возвращаются на один и тот же уровень поверхности.
Нить проходит через два бесконечно малых блока, расположенных на одной высоте, и оба конца свободно свешиваются. Людмила Фирмаль
В общем случае, если точка находится под действием вертикальной силы, которая является функцией a А = 0, В = 0, З = З, откуда З МВ МВ2 МТФ. д = р з ДЗ г = с J п ДЗ. б Горизонтальная поверхность остается горизонтальной surface. In во всех этих движениях локус представляет собой плоскую кривую например, глава 202. 2.Рассмотрим точку M, которая притягивается к неподвижному центру O, по закону, обратно пропорциональному 2 й степени расстояния. Форма притяжения ту. Г2 в, с.
Постоянная, а r расстояние ом. Алгебраический смысл этой силы, которая отсчитывается в направлении ом, равен tg 2,а основная задача этой силы, как видно из пункта 84, равна dr. следовательно, по теореме о кинетической энергии Или в = 2 + фут. Ровной поверхностью является сфера p g = const. Скорость принимает одинаковое число на равных расстояниях от центра притяжения. В общем случае, если точка M находится под действием центральной силы, являющейся функцией r, и алгебраическое значение этой силы, отсчитываемое в направлении OM, равно g г МВ2 МВ2 МВ Д = Ф р д р 2 г = = J В Г р др.
Рассмотрим центроид M, который притягивается к неподвижному центру A по закону, обратно пропорциональному 2 й части расстояния, и отталкивается от неподвижного Центра A пропорционально расстоянию рис.131. Направьте ось Oz вертикально вверх так, чтобы основная работа веса была mg dz. Когда расстояние AM представлено r, алгебраическое значение притяжения A, которое отсчитывается в направлении AM, равно Tr. R2, основная работа dr. наконец, если вы укажете расстояние MA by r, то алгебраическое значение силы отталкивания F , пропорциональное расстоянию, равно tr. Г. Основная работа mp r dr.
По теореме производная d mv2 равна сумме работы составляющих сил, то есть основной работе равнодействующей силы, приложенной к точке д = мг ДЗ д р 4 Мп. Р д р Правая часть этого уравнения является идеальным дифференциалом, поэтому существует функция силы. Это может быть подтверждено заранее на основе теоремы, установленной в главе IV. So, когда мы интегрируем и делим на m Функция здесь должна быть четкой, и скорость будет принимать одно и то же значение каждый раз, когда движущаяся точка проходит через одну и ту же ровную поверхность +4 + = const Это 6 я поверхность. для p они сводятся к сферам.
Смотрите также:
Решение задач по теоретической механике

