Теорема Эйлера
Рассмотрим самый общий случай движения твердого тела и докажем теорему, принадлежащую Эйлеру, о распределении скоростей в твердом теле при произвольном движении. Теорема. Произвольное мгновенное движение твердого тела в любой момент времени может быть представлено как сумма двух мгновенных движений: одного мгновенно-поступательного и одного мгновенно-вращательного. Доказательство. Будем рассматривать движение твердого тела относительно системы осей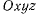 
(рис. 48). С твердым телом свяжем жестко другую систему осей 
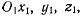относительно которой оно
не совершает движения. Тогда движение твердого тела будет полностью определяться движением подвижной системы координат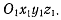 
Выберем произвольную точку М твердого тела и рассмотрим ее движение относительно системы осей 
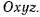Координаты точки М в неподвижной системе отсчета обозначим через 
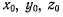а ее координаты в системе, связанной с твердым телом через — 
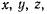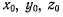Через обозначим координаты точки 
Положение подвижной системы координат определяется положением точки и направляющими косинусами углов между осями подвижной и неподвижной систем координат. Эти направляющие косинусы можно задать таблицей:
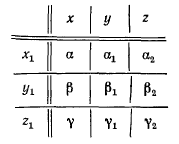
Координаты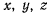 
точки М связаны с ее координатами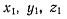 
известными формулами преобразования координат
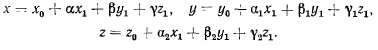
Проекции скорости точки на неподвижные оси координат получим,
дифференцируя координаты 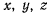по времени,
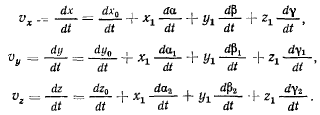
Чтобы придать формулам более симметричный вид, рассмотрим
сначала проекции вектора абсолютной скорости точки М на
подвижные оси Эти проекции найдем из уравнений
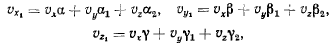
которые приводят к следующей формуле:
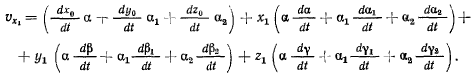
Аналогичным образом можно вывести формулы для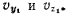 
Дифференцируя тождественное соотношение, связывающее на-
направляющие косинусы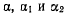 
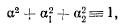
получим
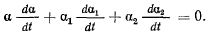
Рассмотрим далее косинусы углов между подвижными осями координат
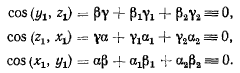
Дифференцируя эти соотношения по времени, приходим к следующему результату:
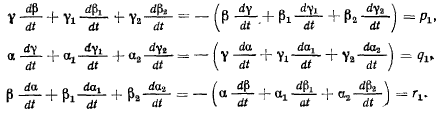
Проекции скорости точки М на оси 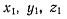запишутся в виде
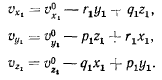
(Последние два равенства легко получаются из первого циклической перестановкой индексов.) Введем единичные векторы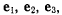 
направленные соответственно по осям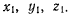 
Тогда вектор v
скорости точки М можно представить как сумму трех векторов
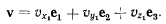
где вектор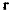 
имеет проекции на неподвижные оси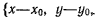 
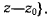
Тогда для проекций скорости получим
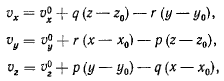
а уравнение винтовой оси в неподвижной системе координат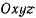 
приобретает вид
Уравнения 
определяют одну и ту же прямую линию— винтовую ось. Но при движении твердого тела мгновенное
распределение скоростей непрерывно меняется со временем. При
этом изменяются величины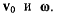 
При непрерывном изменении
коэффициентов уравнения в каждый следующий момент
будут вообще определять уже другую прямую. Геометрическое место мгновенных винтовых осей в неподвижном пространстве 
называют неподвижным аксоидом, а геометрическое место
мгновенных винтовых осей, определенных относительно системы
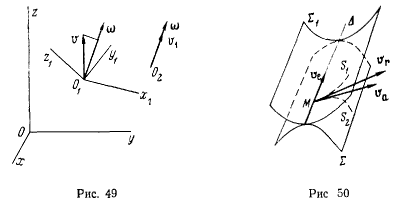
отсчета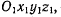 
— подвижным аксоидом. Эти геометрические места (аксоиды) представляют собой линейчатые поверхности, имеющие в каждый момент по меньшей мере одну общую прямую — мгновенную винтовую ось. Покажем, что подвижный и неподвижный аксоиды имеют общую соприкасающуюся плоскость, проходящую через мгновенную винтовую ось. В самом деле, пусть неподвижный аксоид 
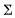и Подвижный аксоид 
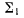имеют общую винтовую ось 
(рис. 50).
Рассмотрим движение некоторой точки М, остающейся все время на
винтовой оси. Пусть S — траектория этой точки на неподвижном
аксоиде X и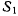 
— траектория точки М на подвижном аксоиде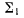
Абсолютная скорость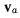 
точки М направлена по касательной к абсолютной траектории точки М. Относительная скорость vr на- направлена по касательной к относительной траектории точки. Переносная скорость — это скорость точки подвижного аксоида, совпадающей в данный момент с точкой М. Но эта точка лежит на винтовой оси, а потому и переносная скорость 
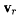направлена вдоль
винтовой оси. Касательная плоскость к неподвижному аксоиду
будет определяться векторами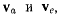 
а касательная плоскость к
подвижному аксоиду — векторами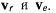 
Но по теореме о сложении скоростей имеем
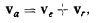
т. е. вектор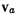 
лежит в касательной плоскости к подвижному аксоду, а следовательно, касательные плоскости совпадают. Непрерыв-ное движение твердого тела можно теперь представить как
качение подвижного аксоида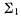 
по неподвижному аксоиду 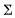с
проскальзыванием вдоль мгновенной винтовой оси.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
