Оглавление:



Теорема Эйлера о крене
Теорема Эйлера о крене. Л. Эйлер доказал следующую теорему: Когда плавающее тело вращается вокруг оси абсцисс Бесконечно малый угол, значение которого не изменяется s. Y. 2 прилегающие участки ватерлинии, которые поддерживают Рисунок 6-4. Район Абэ и акватория Линия. § 6 ^ 2] теорема Эйлера 87 Делится на прямые линии через центр тяжести квадрата Ватерлиния должна соответствовать этому положению.
Смотрите также:
Теорема Эйлера верна для любого бесконечно малого наклонения (крена, дифферента).
Людмила Фирмаль
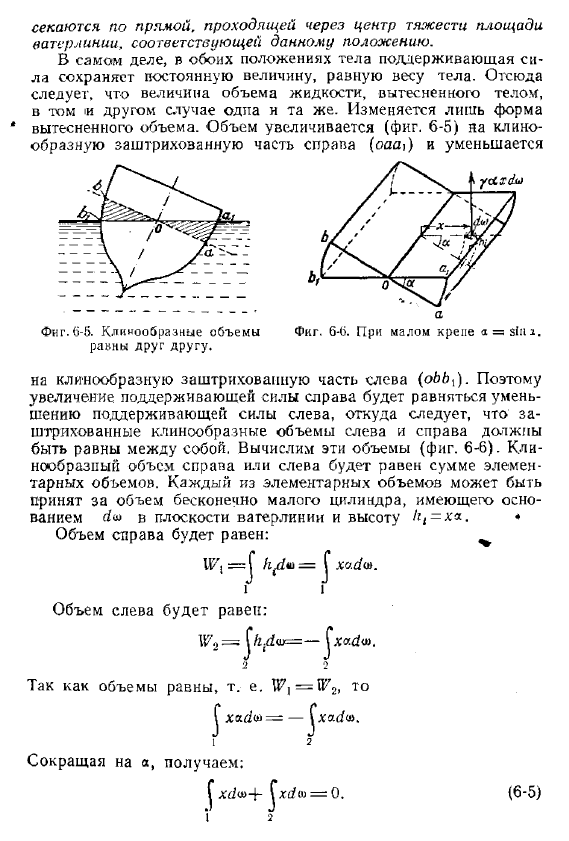
На самом деле, в обоих положениях тела, поддержка Си la поддерживает постоянную величину, равную массе тела. Отсюда Это количество жидкости отодвинутое в сторону организмом В обоих случаях это одно и то же. Меняется только форма Перемещение. Клин увеличивается в объеме (рис. 6-5 Брызг затеняя часть (ОАА) ) и уменьшение Левой клиновидной заштрихованной части.
Смотрите также:
Основы теории плавания. Основные определения. Закон Архимеда.
Увеличение несущей способности с правой стороны Несущая способность слева, откуда Левый и правый штрихованный клиновидный объем Они будут равны друг другу .Рассчитайте эти объемы (рис .6-6) .Каштан Объем справа или слева равен сумме Количество тары .Каждый основной объем Считается, что это объем бесконечно круглого цилиндра с Поверхность воды и высота.
Динамическая остойчивость характеризуется величиной работы восстанавливающего момента, а статическая –величиной самого восстанавливающего момента. Людмила Фирмаль
Громкость на правой стороне выглядит так.И фигура тоже .От 6 до 5 .Рисунок 6-6 заклинивший объем .А = 51т в небольшом крепе .Равны друг другу .Громкость на левой стороне выглядит так: ч . 2 .Потому что объем равен, т . е .^ ^ X и y 1 .Если вы уменьшите его на xc1f {xAsh-0 .(6-5 88 основы теории плавания[Гл . б .Из уравнения (6-6) следует, что статический момент этой области 2 линии воды относительно пересечения двух смежных областей.
Смотрите также:

