Оглавление:





Тензор парной корреляции скоростей и его изменение в пространстве и во времени. Задачи
- Перепад давления, необходимый для прохождения ламинарной области через горизонтальную трубу, представляет собой жидкость с вязкостью 18,3 СР и плотностью 1,32 г » см-3 (в атмосфере с атмосферным давлением убэ радиуса 0,53 см. Какая разница давлений 2 тн будет турбулентной? 5-2 БВР атм-М » 1. Прямая линия 1?^?^ 106-скоростной°сцы турбулентного в НКИ трубы. Длинный поток с гладкой внутренней поверхностью перемещает поток воды.
Внутренний диаметр трубы составляет 15,24 см, перепад давления по длине трубы составляет 4,23•10 «б атм-М-1.Температура системы составляет 20°C. а) определить напряжение сдвига M0 стенки (в dyn-cm-a). б) найти расстояние y / Pmax = 0 от стенки трубы, считая, что поток является турбулентным. 0,1; 0,2; 0,4; 0,7; 0,85 и 1,0.Для расчетов используйте график, показанный на рисунке. 5-3. В) создать полный профиль скорости и представить в виде зависимостей 8 = I-G (p / Pmax). г) выполняется ли условие наличия турбулентности для такого потока? д)Сколько стоит объемный расход?
Для теплообменников стационарных установок наибольшую важность имеет величина поверхности нагрева, так как главным образом от этого зависят и вес и стоимость установки. Людмила Фирмаль
Средняя скорость турбулентного потока в трубе, а) профиль скорости турбулентного потока через гладкую круглую трубу, может быть удобно описан с помощью распределения[1]. (5.80)) Где n-число Рейнольдса. Я не думаю, что это хорошая идея….-4000 110000 3 200000 н 6, 7, 10. Отношение средней скорости к максимальной скорости u2, проверка 2 «2 (n + 1) (2p4-1)) (5.81) Пример выражения (5.4) проверяет правильность этой связи. б) интегрируя логарифмический профиль (5.28) по всему поперечному сечению трубы, находим отношение средней скорости к максимальной скорости (то есть без учета ламинарного подслоя).В чем разница между полученным результатом и формулой (5.81)?
Распределение скоростей по прямоугольному каналу. Жидкость течет в направлении z по прямоугольному каналу с полушириной k (измеренной в направлении y). размер канала в направлении x велик по сравнению с A и принимается p2 = u2 (y).Течение происходит в полностью развитом турбулентном режиме. а) в рамках гипотезы подобия кармана показано, что уравнения, описывающие турбулентное ядро потока, являются: ( / 4 года)* ( / ^ 2)2 (L в 0) (5.82) Касательное напряжение Gdv к стенке. y-расстояние от средней грани канала. B) интегрируйте уравнение (5.82) и убедитесь, что распределение скоростей имеет вид «.Х-п= — л- [б(1-] / т)+ ут](0 ^ р)(5.83) где г * = / М0 / С.
Для интегрирования используйте мнимое граничное условие= — oo для y = k (что объясняет, почему). c) является ли профиль(y) плоским в центре канала(y = 0)? 5-5.В разделе 5.3 мы показали, что можем использовать эмпирическую зависимость между flow3 ^ eTNG потоком импульса и средним градиентом скорости для получения информации о усредненном по времени распределении скорости. Однако возможен и другой подход, основанный на предположении, что турбулентность импульса зависит от расстояния до стенки. Такой подход обычно приводит к гораздо более простому calculations. As в качестве примера рассмотрим течение в кольцевой трубе[21].
Усредненное по времени уравнение движения АТЬ ’ чт0 в турбулентном потоке в трубе выглядит следующим образом: (5.84) (5.85) B) величины m оправдывают утверждение о том, что они являются функциями только r (а не O и r).Указывает, что это утверждение подразумевает отношение dy / db = A. где A-константа. c) введите безразмерное количество (5.86) — Сотовый?- YT° / p-напряжение сдвига стенки. Доказать, что уравнение (5.85) °- Б + Б ^ Т-А — PM in-постоянная величина, связанная с простым соотношением констант a.
Результат Интеграла уравнения (5.87), зависимость ’* И Т. — Т. (5.88) г) определить интегральную постоянную в условии (объясняет физический смысл): C использовать и границы 1 = 0. $ = 1 Конечно. М = 0、 Yf — з = — б, конечно」 (5.89)) (5.90) Преобразуем уравнение (5.88) в конечное выражение 0 = 5 + Один * т. (5.91) функция, которая должна быть интегрирована, если задано m rn1 ^ 1pa (конкретные зависимости, показанные на рис. 5-5, В могут предложить функцию m ( | ) в виде: m =(1-й) ( & -&?* * *) (5.92) Где, при, n-очень большой положительный integer. Is выбранная зависимость m (t) удовлетворительна? Nighty, это соотношение (5.92) приводит к такому распределению скоростей Рот Простите?
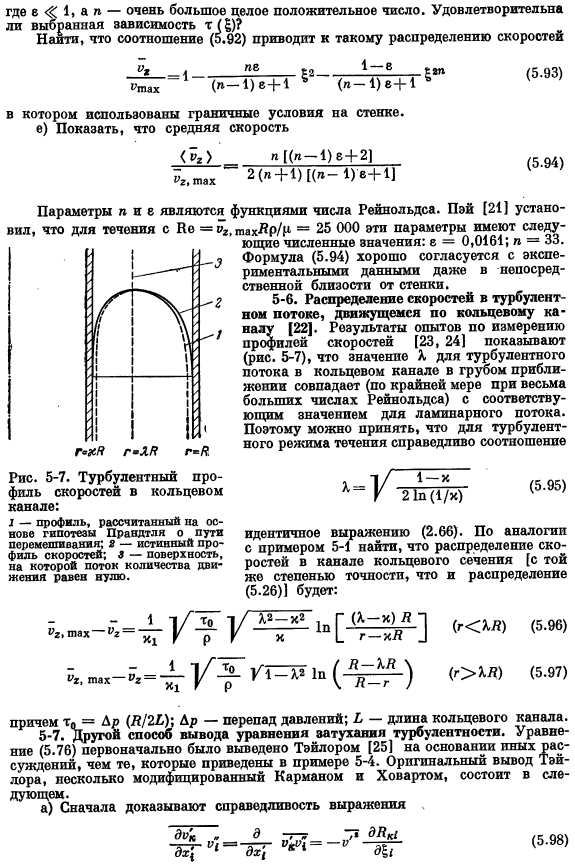
- Если используется граничное условие стенки, д)средняя скорость n [(n-1) 8 + 2) (5.94). Параметры N и E являются функциями числа Рейнольдса. Pei [21]установил, что для потока Be-π> max ^ p / n = 25 000 эти параметры имеют: 5-7.Турбулентный профиль скорости в кольцевом канале: 1-профиль, рассчитанный на основе гипотезы Прандтля о пути смешения. 2-истинный профиль скорости. Ч-поверхность, где поток импульса равен нулю.
Число: e = 0.0161; n =33. Уравнение(5.94)хорошо согласуется с экспериментальными данными даже в непосредственной близости от стенки. 5-6.Распределение скоростей турбулентности, движущейся по кольцевому каналу[22].Экспериментальные результаты по измерению профиля скорости[23, 24] (рис. 5-7) показывают величину турбулентного течения в кольцевом канале шероховатости approximation. It показано, что (в случае хотя бы очень большого числа Рейнольдсов) совпадают соответствующие значения ламинарного течения.
Для систем охлаждения машин указанного типа важно иметь как можно меньшую лобовую поверхность, так как именно последняя определяет любое сопротивление системы охлаждения. Людмила Фирмаль
Поэтому можно предположить, что в турбулентном режиме существуют следующие соотношения: (595) Аналогично выражению (2.66). по аналогии с примером 5-1 можно видеть, что распределение скоростей[5.26]в кольцевом канале имеет ту же точность, что и распределение: «.- Б-А-ГТЛГ1. (^^г) (г ся) (5.96) (г> АУ) (5.97)) Кроме того, T = = Dp (H / 21); Dr-перепад давления; B-длина кольцевого канала. 5-7.Еще один способ получить уравнение затухания турбулентности.
Уравнение(5.76) было первоначально выведено Тейлором [5] на основе соображений, отличных от приведенных в Примере 4-5.Оригинальный вывод Тейлора, несколько модифицированная Каллмана и Хауорт, находится: а) сначала докажите правильность формулы (5.98) б) тогда обе стороны уравнения (5.98) дифференцируются относительно x]. 。 d » 1 _ d, _ TT * ^ Hk1 добро пожаловать на наш сайт. ДХ] ДХ [*Д ^ 1 (£5.99)) в) используя соотношение (5.99), можно увидеть, что если точки B ’и B *совпадают, то выражение может быть применено. _ _- Г ’(d2VK1 \ ДХ \ ДХ] \ Н1-1 (5.100) г)в случае изотропной турбулентности вычисляется уменьшение кинетической энергии потока за решеткой.
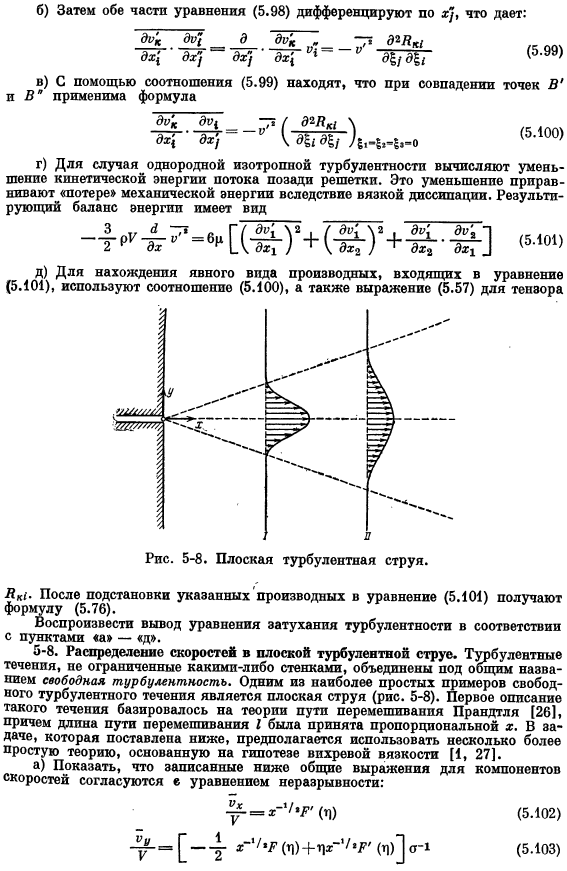
Это уменьшение эквивалентно»потере» механической энергии из-за вязкой диссипации. Результирующий энергетический баланс Д) для нахождения явной формы производной, входящей в уравнение (5.101), воспользуемся соотношением (5.100) и уравнением тензора (5.57 Рис. 5-8.Плоские турбулентные струи. БК(.Подставляя производную, указанную в Формуле (5.101), получаем формулу(5.76). Он воспроизводит вывод уравнения ослабления турбулентности в соответствии с пунктом » А » 〜 «Е».
Распределение скоростей плоской турбулентной струи. Турбулентность, не ограниченная стенами, объединяется под общим названием Свободная турбулентность.1. одним из простейших примеров свободной турбулентности является плоская струя (рис. 5-8).Первое описание такого течения было основано на теории смешивающего пути Прандтля[26], где длина смешивающего пути I была пропорциональна x. In в вопросах, затронутых ниже, предлагается использовать несколько более простую теорию, основанную на гипотезе вихревой вязкости [1, 27].
Указывает, что общая формула компонента скорости, которая записана ниже, согласуется с уравнением неразрывности. =(северный) год=- [—- (5.102) (5.103) В этих формулах V представляет некоторую (еще не заданную) характеристическую скорость, а величина m / = o (y / x) является безразмерной комбинацией независимых переменных(o-произвольная константа). б) исходя из Формулы (5.102), определить, что объемное течение AG-составляющей импульса через плоскость, перпендикулярную оси x (например, через плоскость I или плоскость 7/), не зависит от X. в) если турбулентная вязкость Ve= =(P / p предполагается пропорциональной x ’ ^ 9 (т.
То усредненное по времени уравнение движения будет иметь вид: (5.104) D) уравнение: используя соотношения (5.102) и (5.103), уменьшите уравнение (5.104)=°(5-105 Любые константы k и o входят в последнее уравнение в виде произведения, поэтому сумма q *!Для удобства можно установить значение x/ =°(5A06) e) установить, что уравнение (5.106) признает тройной интеграл и что результат Интеграла выглядит следующим образом: (5.107) f) выведите формулу (5.108) Куда? И 7 = р г — Утвердительный ответ. (5.109) если установить значение o равным 7,67, то уравнение (5,108) полностью объясняет имеющиеся экспериментальные данные вплоть до значения Q, близкого к 1,5.
Смотрите также:

