Оглавление:










Тензор парной корреляции скоростей и его изменение в пространстве и во времени (уравнение Кармана — Ховарта)
- В разделе 5.2 было установлено, что усреднение уравнений движения по времени приводит к появлению в нем дополнительных членов, которые могут быть описаны в виде производной тензора напряжений Рейнольдса pr ^ V/. Усредненное произведение характеризует «корреляцию» между этими пульсациями, поскольку величины V /и r> /являются пульсациями скорости в I и/или направлении, взятыми в одной и той же точке. За последние 20 лет были предприняты интенсивные попытки создать метод теоретического расчета корреляции между пульсациями в двух различных точках. Указанные корреляции, которые можно найти эмпирически, несут информацию о размере и направлении турбулентных вихрей.
Скорость пульсации в 2 различных точках B и 3 корреляции, связывающие давление, описаны в выводе ниже. Сумма, связанная с точкой B, равна 1 Штриху сверху, а сумма, связанная с точкой B, обозначается двумя линиями» .Рассмотрим 3 типа корреляций, определенных следующим образом: Пульсация давления и пульсация в точке B (- компонент скорости в точке B’、 оо) — (/- компонент 2-го ранга Tensor. It представляет собой корреляцию между пульсациями скорости в точке B ’и B«. — (/«- Компонент тензора 3-го ранга, характеризующий корреляцию между 2 пульсациями скорости в точке B и 1 пульсацией в точке B.».
При сравнении различных расположений труб в пучках по энергии, необходимой для движения воздуха через пучок в системах охлаждения таких машин, как самолеты, автомобили, локомативы и пр. Людмила Фирмаль
Характеристики этих корреляций были подробно исследованы для случая изотропной однородной турбулентности сплошных сред (r = 0). в этом простейшем случае дальнейшее обсуждение будет ограничено. Изотропия турбулентного течения означает, что при вращении осей координат или при отображении зеркального изображения на плоскости, проходящей через начало координат, усредненные по времени значения компонент скорости и их пространственных производных в любой фиксированной точке в конкретной системе координат не изменяются. change. In в частности, изотропное свойство подразумевает реализацию отношения. я * = = в= = в’*; = 0.
По определению, однородная турбулентность потока, в котором разные усредненные по времени величины не зависят от пространственных координат. Так, в однородном турбулентном потоке, о ’= в’. Теоретические исследования[141] показывают, что, рассматривая течение в системе координат, движущейся со средней скоростью, поток за однородной сеткой может достигать потока, близкого к локально однородной изотропной турбулентности с потоком жидкости или газа за однородной сеткой. В изотропной турбулентности введенная корреляция может быть выражена в следующей безразмерной форме: (5.38) (5.39) В этом разделе мы выводим уравнения парного корреляционного тензора VT.
По этой причине для каждой из 3 корреляций(Р お お и Т₁/к), 1) найти ненулевую компоненту, применяя изотропное свойство и анализируя конкретные случаи, когда точки B ’и B1 находятся на одной оси XY (рисунок).5-4); 2) установить общую форму корреляции. Эта форма должна гарантировать, что указанная корреляция имеет необходимые характеристики преобразования. 3) основываясь на уравнении непрерывности, мы находим отношения, которые связывают компоненты различных корреляций друг с другом. Затем, используя уравнение Навье-Стокса, выводится уравнение кармана-Хауарта, которое объясняет поведение тензора парной корреляции[14, 15].
В следующем представлении показано положение точки B с координатой x’c и положение точки B с координатой X/. для указания расстояния между точками B ’и B используйте вектор R с компонентами components =х1-х\(рис.5-5). Корреляция P,.Во-первых, рассмотрим частный случай, когда точки B ’и B «находятся на одной оси xx. Поскольку турбулентность изотропна, anak изменяется, когда система координат поворачивается на 180 градусов вокруг оси, поэтому p’R> 2 и p’R? Среднее значение S должно быть потеряно. Единственная ненулевая составляющая изотропного вектора P₁ может зависеть только от r и I.
Векторное выражение справа от соотношения 1 = 1 (5.41) выглядит следующим образом: Также из этого выражения следует Pr = P,= 0.Поскольку формула(5.42) преобразуется в векторную величину, то она является общей формулой для Pr с любым расположением точек B ’и B». Напишите уравнение неразрывности скорости в точке B: ⁽⁵ЛЗ⁾ Поскольку пульсация давления p ’ зависит только от x /и I, ее можно ввести в уравнение (5.43)под знаком производной.
Если вы усредните левую часть данного уравнения с течением времени и умножите на p’, вы получите: 2-4 ^ =° 2’аг? Аварийное реагирование.⁾ Подставляя выражение (5.42) в выражение (5.45), получаем следующее дифференциальное уравнение для функции a (r, I): — ± =0(5.46) Решением этого уравнения является функция a = C / g3.In в физическом смысле функция a ® равна r-* 0. Он должен быть конечным, как 0.It из вышесказанного ясно, что интегральная константа C должна быть равна нулю, так как функция C / r3 бесконечно возрастает с уменьшением r.
Отсюда соотношение А = 0 или/> 4 = 0(1 = 1、2、3)(5.47) Из уравнения (5.47) следует, что пульсации давления в любой точке изотропной однородной турбулентности и пульсации скорости в других точках не коррелируют друг с другом. Рассмотрим случай нахождения точек B ’и B на той же оси x, что и до корреляции постоянного тока. Из-за изотропии поля скоростей турбулентного потока должны выполняться следующие соотношения:= r4 ″ z = 0, эти средние значения равны изменяет знак при повороте на 180°вокруг оси X. х₃р₃ = х₃х₂ = 0.Это связано с тем, что вам нужно изменить знак при зеркальном отображении в плоскости(^ 1, x.).
- Остальные ненулевые компоненты являются функциями T и I. Поэтому вы можете написать: (1 = 2, 3) Если точки B ’и B» BC имеют вид: ось xx, помещенная в матрицу / 00 0-й 0 Около 0-го (5.50 )) Эта матрица может быть представлена в виде суммы 2 матриц. / — 1ОО1 о о о |о о / (5.51)) Правая часть соотношений (5.48) и (5.49) содержит Н₁₁ и яза как компоненты, а остальные компоненты (я, yat 1+ 1) равны уравнению 2-го тензора л/ Ноль, БК = д(р, 1) 6С + м(р, 1)(5.52) Поскольку значение(5.52) преобразуется как Тензор 2-го ранга, то это общая формула тензора Bt для любого расположения точек B ’и B«.
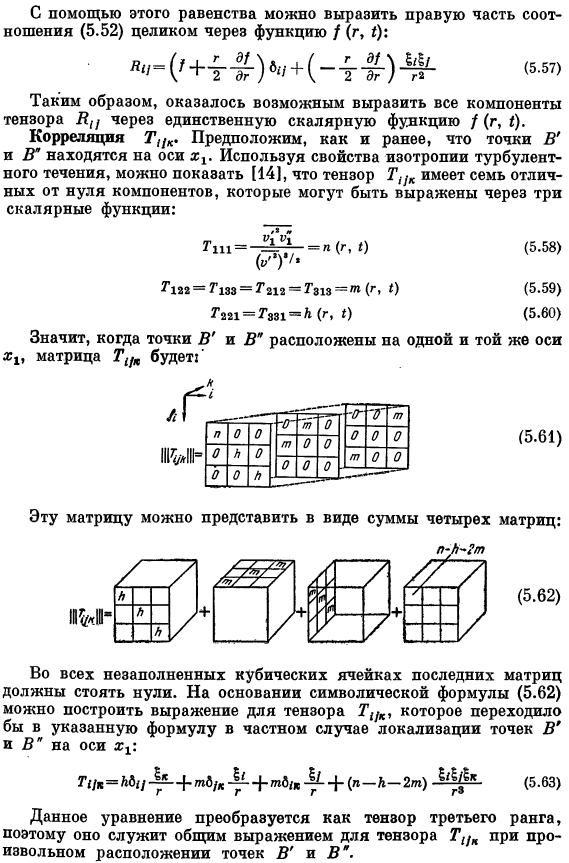
Как и прежде, рассмотрим уравнение неразрывности скорости VI в точке B (5.43), и в этом уравнении 2’х «м» ⁽ Если мы разделим это уравнение на V и усредним его во времени, то получим: 2 ’^ ⁵ ’L /’ ⁰ (5.54) 2-4гл⁾ После присвоения явной формы тензора (5.52) выражению (5.55) Получается следующее соотношение: (5.57)) Используя это уравнение, правая часть соотношения (5.52) может быть полностью представлена функцией/(r, ()). n » = (/+T’1r) в»(- Таким образом, мы смогли выразить все компоненты Уникальной скалярной функцией тензора/(r, I). Корреляция Т₁ / k. As прежде мы предположим, что точки B ’и B «находятся на оси X.
В последнее время собрано много экспериментального материала по компактным теплообменникам, имеющим большие теплообменные площади, приходящиеся на единицу объема. Людмила Фирмаль
Используя турбулентную изотропию, можно показать, что Тензор T₁ / ₁ имеет 7 ненулевых компонент, которые могут быть выражены в 3 скалярных функциях: Gm-G1z3 = G212 = Tz1n = m (r, 1) (5.59) Эта матрица может быть представлена в виде суммы 4 матриц. Можно создать Тензорные выражения Tn / k. Это находит отражение в специфическом конкретном случае точки B^ Это уравнение служит общей формулой тензора TT при любом расположении точек B ’и B’, поскольку оно преобразуется как Тензор 3-го ранга.
Если вы используете уравнение непрерывности и выполняете аналогичную операцию, как указано выше, вы можете легко увидеть, что отношения m, n и A связаны следующими отношениями: используя приведенное выше уравнение, правая часть(5.63) может быть представлена одной функцией A(r, 4). Теперь, если мы используем уравнение Навье-Стокса и рассмотрим V = 0, мы можем вывести уравнение тензора Bj. Для этого мы пишем уравнение, которое должно удовлетворять 4-компонентной скорости вблизи точки B’. Умножьте уравнение(5.65) и учтите p’r> ^ = 0, чтобы выполнить усреднение по времени. При выводе последнего соотношения использовалось уравнение неразрывности= 0.
Аналогично, умножив уравнение K-ой составляющей скорости вблизи точки B на»»и усреднив по времени、 Вы можете напечатать следующую формулу: Т-2-4:’ -’ 2 а? (5.67) Добавление уравнений (5.66) и (5.67) для каждого члена приведет к: (И’ ** (5.6 Как видно из Формулы (5.68), парный корреляционный Тензор B₁k может быть найден только в том случае, если известен тройной корреляционный Тензор Tck. Этот тенор может указывать на то, что он удовлетворяет дифференциальному уравнению, содержащему корреляционный Тензор 4-го порядка, и т. д. В результате получается бесконечная последовательность выражений, которые»связываются» одно за другим с корреляционной функцией.
Чтобы найти корреляции любого порядка, включая B₁KK, нужно решить всю бесконечную последовательность корреляционных уравнений вместе, строго говоря. Теперь мы выполняем так называемую операцию «складывания» уравнения (5.68).То есть ставим r = k и добавляем результат с индексом. Из соотношений(5.57) и (5.64) видно, что сумма 2 и 2 ТМ является выражением. 2л»=(3+ г- |)/(5.70) (5.71) Подставляя эти выражения в Формулу (5.69), замените операторы Y, d2/ D5 эквивалентным оператором[d2/dg24-(2 / g) d / dg], описанным в сферических координатах.
После ряда преобразований получим следующее уравнение: (Z g4 -) [- zg» «/ +2^ gu, g (t + 4 -) А2⁷’/] (5.72) Интеграл этого выражения указывает, что выражение в скобках равно C /g3.treC-это интеграционная константа. константа C должна быть установлена в ноль, потому что сумма членов в скобках не становится бесконечностью, как в r — > 0.So, в итоге вы увидите следующее: Уравнение (5.73) объясняет поведение бинарной корреляционной функции f (r, I) и называется уравнением кармана-Хауарта.
Измерив функции f, H и используя спидометр горячего воздуха, мы обнаружили, что уравнение (5.73) удовлетворяет экспериментальной погрешности[16].Некоторые авторы [2] считают такое хорошее соответствие теории и эксперимента доказательством обоснованности использования уравнения Навье — Стокса в качестве начального приближения при описании турбулентности. На рисунке 5 показан общий вид кривой, описывающей поведение функций/, α и Λ. 5-6.Площадь кривой/®, то есть Y / ® Λ характеризует размер турбулентных вихрей. Этот размер называется шкалой турбулентности.
В литературе имеются многочисленные исследования, посвященные изучению уравнения преобразования Фурье (5.73) [14, 171].Для многих ограниченных случаев было получено решение, передающее полезную информацию о структуре турбулентного потока. Читатели могут узнать больше о современном состоянии теории турбулентности, прочитав книги по турбулентности[2, 18-20], а также оригинальную работу, приведенную выше. Цифры 5-6.Общие характеристики поведения функций/, I и K. Микромасштабность Тейлора турбулентного X определяется пересечением парабол, аппроксимирующих функцию y ® малого.
Пример 5-4.Zahnio thabboul PocketT-Х Вот как это делается: И Λ=0./(r, 0-четная функция аргумента r, а точка r = 0, поэтому эту функцию можно представить в виде разложения. /(r,*)= 1 + гггг ’ + −4- (5.77)) В литературе микроскопический смысл того, что хорошо известно Здесь мы ввели шкалу ранга профессионал Выходная турбулентная решетка Ханьи М Где A-числовой коэффициент константы. Назначить выражения (5.77) в выражение (5.76) и заменить оператора / L1 с эквивалентный оператор В (А / топор).Где V-координата и [электронная почта защищена] / p-mm h, это необходимо со стороны турбонаддува[5.3).Как? Вперед турбо 5-4.
Смотрите также:

