Оглавление:



Температурные зависимости ползучести и длительной прочности.
- Ползучесть и долговременная температурная зависимость Силы. Тот же закон можно применить и к твердым атомам, находящимся в состоянии беспорядочного теплового движения по отношению к молекулам газов. Распределение энергии между газами молекул
устанавливается законом Больцмана. Если энергия теплового движения находится в диапазоне U — \ — d U, который является относительным числом атомов, выраженным как dq, то по формуле Больцмана йд=±^^-^д У. (193.1) Где K-постоянная Больцмана, а T-абсолютная температура. Уравнение (193.1),
в котором энергия превышает определенную величину, называемую энергией Людмила Фирмаль
активации, указывает, что определенное число атомов с большей энергией, чем энергия активации, всегда присутствует и поэтому движется через кристаллическую решетку, чтобы атом металла, вызывающий тепловое колебание, покинул свой узел и проник между соседними атомами. Указывая относительное число атомов,
активированных Q, понятно =Дж к Т Е Р К? Д У= = Е Х р К т т Ио Если процесс ползучести определяется в первую очередь высвобождением дислокаций, вызванных тепловым движением атомов (вторая фаза ползучести), то скорость ползучести-§ 193]определяется температурой ползучести 433. При этом напряжении вибрация пропорциональна величине q*, поэтому e=T)=e x p f-va (a), (193.2) энергия активации C70
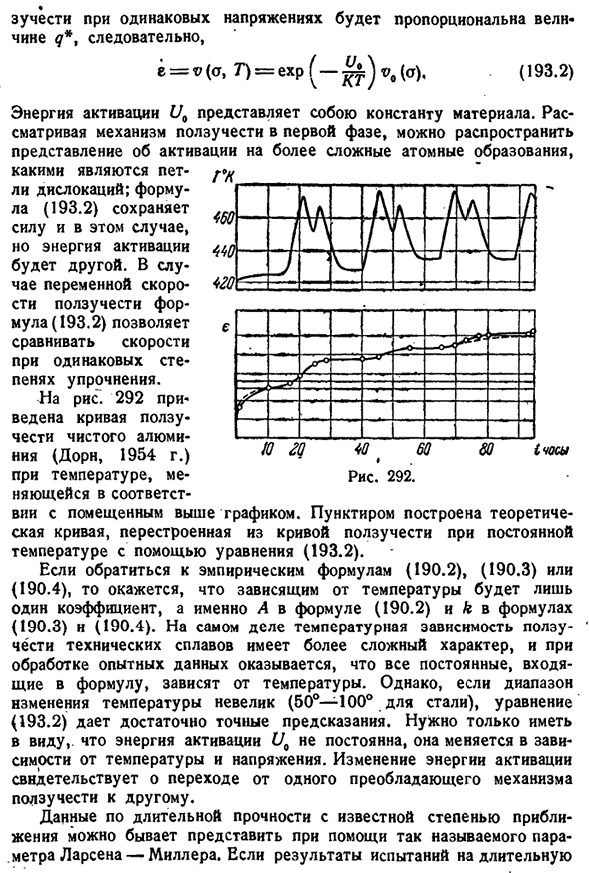
- является константой материала. В этом случае формула (193.2)остается в силе, но энергия активации отличается. Для переменных скоростей ползучести формула (193.2)позволяет сравнивать скорости при одинаковой степени упрочнения. Для риса. 292 показана кривая ползучести чистого алюминия (Dawn, 1954) с температурами, изменяющимися в зависимости от движения, размещенного сверху. Теоретическая кривая (193.2), восстановленная
из кривой ползучести при постоянной температуре, создается пунктирной линией. Обратившись к эмпирической формуле (190.2), (190.3) или (190.4), можно увидеть, что она зависит только от температуры, то есть от А и к Формулы (190.2) и формулы (190.4). На самом деле температурная зависимость ползучести технического сплава более сложна, и при обработке экспериментальных данных оказывается, что все константы, содержащиеся в Формуле, зависят от температуры. Но если диапазон температур мал
(50 ° −100°для стали), то уравнение (193.2) дает достаточно точный прогноз. Следует Людмила Фирмаль
отметить, что энергия активации с не является постоянной и изменяется в зависимости от температуры и напряжения. Изменение энергии активации свидетельствует о переходе от одного доминирующего механизма ползучести к другому. Данные о длительной прочности с определенной степенью приближения легко могут быть представлены так называемым параметром Ларсена-Миллера. 436 ползучесть и долговременная прочность[гл.
XVIII Величина с расширяет все испытываемые точки для натяжения по одной оси (ILN, обычно логарифмическое натяжение), а затем размер T (C-/-logT), затем различные температуры и различные деформации. Долгосрочная прочность материала может быть определена при любой температуре с помощью параметра Ларсена-Миллера.
Смотрите также:
| Процесс ползучести | Феноменологические теории одномерной ползучести |
| Длительное разрушение | Релаксация напряжений |

