Оглавление:
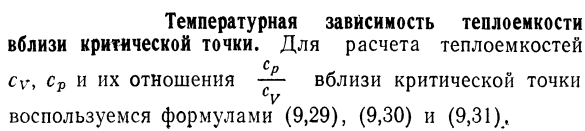


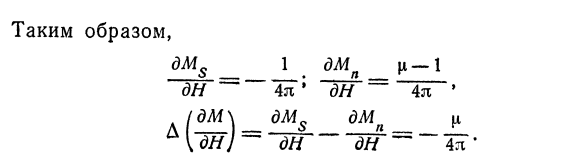

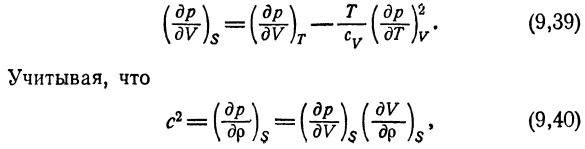

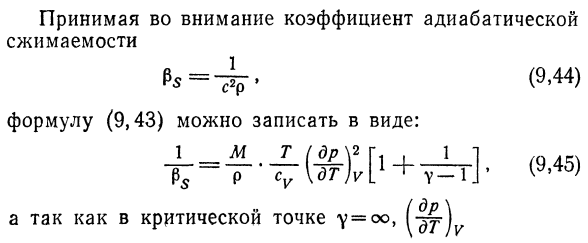
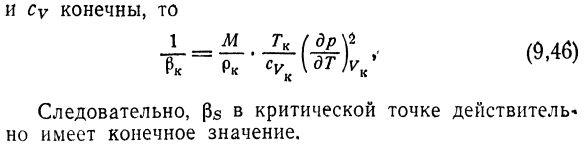

Температурная зависимость теплоемкости вблизи критической точки.
- Температурная зависимость теплоемкости Рядом с критической точкой. Для расчета теплоемкости Брак cv, cp и их взаимосвязь-около критической точки Используйте формулы(9.29), (9.30) и (9.31) T Cf. кал / г град 90.- 70.- Пятьдесят- Ов, Дж / град / У 230235240245250 Т°С Рисунок 52. Зависимости Y и cf Температура является важным Площадь метилового спирта.
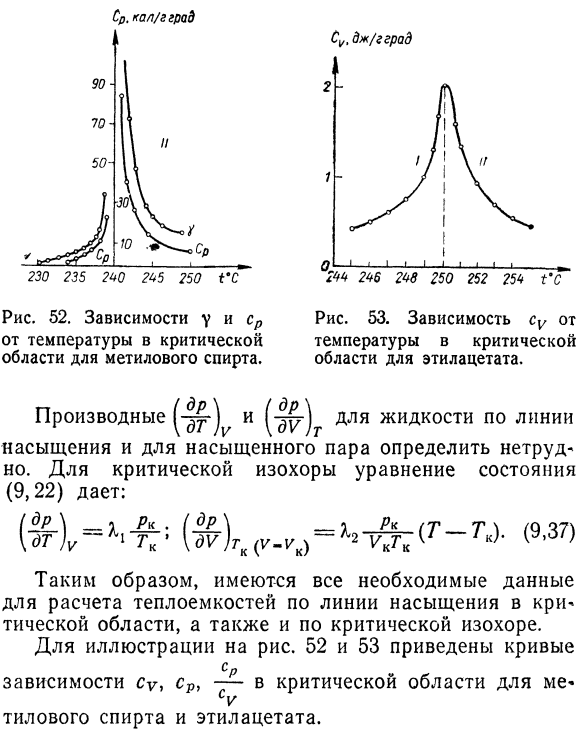
Производная I〜) и 244246248250252254 t’c Диаграмма 53. ЧВ зависимости Критическая температура Зона этилацетата. W ^жидкость вдоль линии Насыщенный и насыщенный пар легко определить по нему Не сложный. (9.22): Поэтому все необходимые данные имеются. Рассчитайте удельную теплоту на насыщенной линии при Критическая область, критические IsoCore.
Для критического значения, уравнение состояния Людмила Фирмаль
Для иллюстрации 52 и 53 приведены кривые Зависимости cv, cp, — * — важные области для меня* Сью. Этиловый спирт и этилацетат. O9 D задачи и упражнения 1.It показано во время фазового перехода Первые типы A и ПТ бесконечны. Вам нужно использовать знаковое уравнение Формула(9.3). 2.Предположим, что теплота перехода K постоянна Показано, что давление насыщенного пара изменяется экспоненциально с температурой Новый закон.
Решение. Ш ^ т (В2-ЧХ)’ Где V \ — объем жидкого моля, далекий от критического Точка, v2-молярный объем пара, находящийся далеко от критической точки ки, П2 ^> ВЛТ Предположим, что насыщенная пара удовлетворяет выражению Уравнение Клапейрона, уравнение (9.38), представленное по ошибке Закручиваться: ДП ХР ~ ~ 9 Откуда Р = const е-ю 3.Определить скачок теплоемкости
- Переход проводника (например, олова) из сверхпроводимости Из сверхпроводящего состояния в нормальное состояние. Предполагая решение, выражение (9.12)、 Получаем около Y = I, x = M, скачок теплоемкости. Ан \ 2 (ДМ \ Для нормальных проводников с —1 Для сверхпроводников И так оно и есть.、. = Я» (США Подобный этому 1 «ш | л-1 н ДУ〜4Л * ДУ-4-й ДМС ДМП _ с 224 но q = 1 + 4l: x, а x-парамагнетик и антиферромагнетик
Вещество 10-5-10-6 порядка. ) = — W и^ — cd = 41) Этот результат действителен только в том случае, если: Внешнее поле#c = = 0.Когда проводник преобразуется в NSFO Это сопровождается нагревом до сверхпроводящего состояния. Эффект, то есть в данном случае фаза ne Первый вид перехода описывается уравнением Клапейрона- Клавдий. 4.Пример Гаса Ван дер Вааль Сауве* Степень сжатия (f-j -) и коэффициент*
Коэффициент теплового расширения в критической точке (- gf-j до бесконечности. 5.Показать его доктор. (др. дв.(доктор 6.Используя уравнение состояния Кри* Площадь (9.22), определяемая производными ДТ) г и ДВ) Т По линиям насыщения жидкостью и паром. 7.Скорость звука.
Критическая точка имеет конечное значение. Решение.55) я из отношения Б Е, 62) можно получить: (д-р \ _ (др \ т(д-р \ * И я думаю, что 225 и обмен К м потому что это v = — так как: Или ДТ) в Пятьдесят пять — Я. Один От/до дифференциальный клапан И Один в- в \ ш)т (вес (9.41) •(9,42) Критическая точка 7=°. («^р) и CF остаются Finite. So … 2 _ МТК(д-р 8.
Адиабатический коэффициент Адиабатическая сжимаемость в критической точке конечна Окончательное значение. Solution. In предыдущая задача Получены термодинамические соотношения: Учитывайте адиабатический коэффициент Степень сжатия Формулу (9.43) можно записать в виде Дж, если т(г ПС-п » Су \ ДТ)г (9.44) ±T•(9 45 45) И в критической точке г = ОО> {«ш Двести двадцать пять И Су конечна. Поэтому ps в критических точках Это действительно важно.
Смотрите также:
Решение задач по термодинамике
| Уравнение состояния критической области. | Расширенная формулировка теоремы Нернста. Третье начало термодинамики. |
| Теплоемкость в критической области. | Получение низких температур. |

