Задача №4
Тело вращается вокруг неподвижной оси по закону
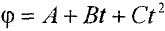 (рад), где
(рад), где 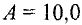 рад;
рад; 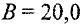 рад/с;
рад/с; 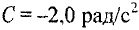 . Расстояние от точки до оси вращения
. Расстояние от точки до оси вращения 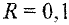 . Найти полное ускорение материальной точки в момент времени.
. Найти полное ускорение материальной точки в момент времени.
Дано: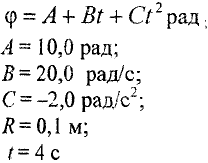
Найти: 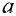
Решение:
Полное ускорение 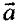 точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения
точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения 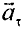 , направленного по касательной к траектории, и нормального ускорения
, направленного по касательной к траектории, и нормального ускорения 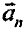 , направленного к центру кривизны траектории (рис. 2.1),
, направленного к центру кривизны траектории (рис. 2.1), 
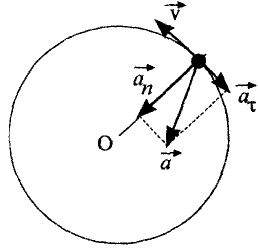
Так как векторы 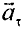 и
и 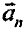 взаимно перпендикулярны, модуль ускорения
взаимно перпендикулярны, модуль ускорения
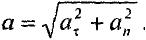
Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами
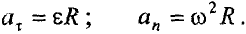
Подставляя выражения 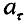 и
и 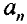 в формулу (2.1), находим
в формулу (2.1), находим
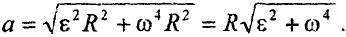
Угловую скорость 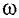 найдем, взяв первую производную от угла поворота по времени
найдем, взяв первую производную от угла поворота по времени
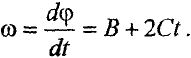
В момент времени 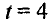 модуль угловой скорости
модуль угловой скорости 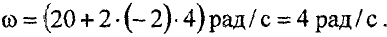
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени
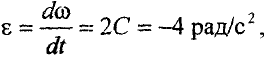
т.е. движение равнозамедленное при 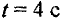 .
.
Подставляя значения 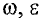 и
и 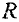 в формулу (2.2), получим
в формулу (2.2), получим 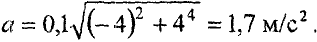
Ответ. 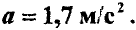
Эта задача взята со страницы задач по физике с решением:
Возможно эти задачи вам будут полезны:

