Пример решения задачи №63.
Тело соскользнуло по желобу с высоты Н без начальной скорости и описало петлю радиусом R в вертикальной плоскости (рис. 15-7). Если трение отсутствует, то суммарная потенциальная и кинетическая энергия в любой точке траектории одинакова и равна начальной потенциальной энергии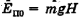 
в высшей точке. По закону сохранения механической энергии 
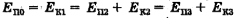и т.д. или
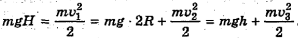
Решение:
Для решения задачи можно выбрать любое из этих равенств в зависимости от данных и искомых величин, а также начальных и граничных условий.
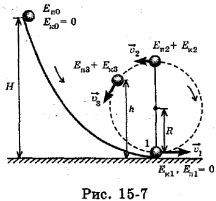
Иногда требуется определить работу силы тяжести на определенном участке траектории. Эта работа всегда равна разности потенциальных энергий в конце этого участка и в начале его, взятой со знаком «минус». Или она равна изменению кинетической энергии, взятой со знаком «плюс». Так, в примере 1 работа А силы тяжести при падении тела с высоты Н до высоты h
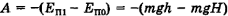
или
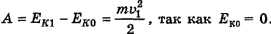
Если на движущееся тело действуют внешние силы, то их работа на некотором участке траектории равна разности полной механической энергии в конце участка и в его начале. То же самое будет, если в замкнутой системе между телами действуют силы трения или сопротивления. В этих случаях сумма кинетической и потенциальной энергий тела в каждой последующей точке траектории меньше, чем в предыдущей, из-за потерь механической энергии, превращения ее во внутреннюю (тепловую) энергию. Для определения работы сил трения надо из суммы потенциальной и кинетической энергий в конце участка траектории, на котором эта работа определяется, вычесть сумму потенциальной и кинетической энергий в начале этого участка. Например, в случае, изображенном на рис. 15-2, а) при действии между скатывающимся телом и наклонной плоскостью на всей ее длине силы трения работа этой силы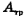 
может быть определена равенством 
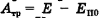где Е — полная механическая энергия в данной точке. У основания наклонной плоскости 
.
Работа силы трения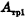 
на участке между точкой 1 и основанием наклонной плоскости
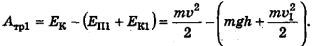
Понятно, что эта работа всегда будет отрицательна, так как полная механическая энергия тела в конце участка меньше, чем в его начале, из-за потерь на трение. Если же на движущееся тело действуют внешние силы, увеличивающие его механическую энергию, то работа этих сил может быть положительна.
Если на систему тел действуют внешние силы и в самой системе действуют внутренние неконсервативные силы (силы трения, сопротивления), то суммарная работа этих сил равна изменению полной механической энергии системы, т. е. равна опять же разности суммарной механической энергии в конце процесса и в начале его.
Если в задаче что-нибудь сказано о КПД (коэффициенте полезного действия) какого-либо механизма или машины (дан или спрашивается), то начинать решение задачи удобно с формулы КПД. Напомним, что КПД механизма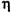 
называют отношение полезной работы 
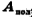совершенной этим механизмом, ко всей затраченной работе 
КПД выражают в процентах:
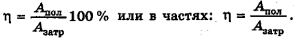
Только не путайте КПД с потерями энергии. Если сказано, что потери энергии 20%, то КПД равен 80%.
Поскольку за счет совершенной работы изменяется кинетическая или потенциальная энергия тела, то в числителе или знаменателе последней формулы вместо полезной или затраченной работы может стоять изменение кинетической или потенциальной энергии. При этом возможно в этой формуле сочетание работы (полезной или затраченной) с изменением потенциальной или кинетической энергий тела или кинетической энергии с потенциальной. Например, если тело имело на некоторой высоте потенциальную энергию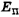 
, а упав на землю, совершило работу за счет части этой энергии, то формула КПД 
.
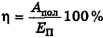Здесь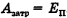 
, так как на земле потенциальная энергия тела равна 0.
Может быть наоборот, когда за счет совершенной работы тело приобрело потенциальную энергию, например, взлетело на высоту или упруго деформировалось. В этом случае
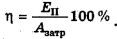
Здесь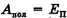 
.
Если тело, бывшее в состоянии покоя, за счет затраченной работы приобрело кинетическую энергию, то формула КПД
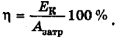
Здесь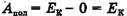 
(поскольку кинетическая энергия тела, бывшего сначала в состоянии покоя, равна 0).
Если кинетическая энергия летящего тела частично превращается в его потенциальную энергию, то формула КПД
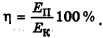
Может быть наоборот, когда тело, благодаря запасу потенциальной энергии (например, падая с высоты), приобрело кинетическую энергию. В этом случае
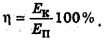
Следует отметить, что в числителе или знаменателе этой формулы вместо работы или механической энергии может также стоять количество теплоты Q полезное или затраченное.
Таким образом, в числителе или знаменателе формулы КПД могут быть записаны следующие величины, имеющие одинаковую единицу измерения — Дж: работа, потенциальная энергия, кинетическая энергия, полная механическая энергия, количество теплоты Q, равное изменению внутренней энергии тела 
. Выбор каждой из этих величин в каждом конкретном случае зависит от условия задачи.
В теории удара рассматриваются два предельных вида соударений: абсолютно упругий и абсолютно неупругий удар. Оба этих взаимодействия представляют собой пример физической абстракции. Тем не менее теория абсолютных упругого и абсолютно неупругого ударов имеет важное значение при практических расчетах, выполняясь тем точнее, чем ближе реальное соударение тел к абсолютно упругому или абсолютно неупругому удару.
Абсолютно упругим ударом называется удар, при котором механическая энергия тел не превращается в их внутреннюю энергию. При этом ударе кинетическая энергия тел частично или полностью превращается в потенциальную энергию их упругой деформации, которая затем полностью снова превращается в кинетическую энергию. При абсолютно упругом ударе между телами действуют только консервативные силы упругости, благодаря чему не происходит потерь механической энергии (имеется в виду, что система соударяющихся тел замкнута). Поэтому при абсолютно упругом ударе выполняются оба закона сохранения: закон сохранения импульса и закон сохранения механической энергии (точнее кинетической энергии).
Рассмотрим применение законов сохранения импульса и механической энергии для определения скоростей двух шаров после центрального абсолютно упругого удара, при котором прямолинейная траектория шаров проходит через их центры. Пусть масса первого шара 
его скорость до удара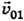 
, его скорость после удара 
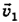, масса второго шара 
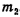, его скорость до удара 
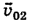, его скорость после удара 
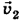(рис. 15-8).
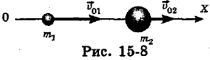
По закону сохранения механической энергии сумма кинетических энергий шаров до соударения равна сумме их кинетических энергий после соударения:
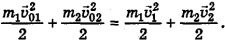
Кроме того, по закону сохранения импульса суммарный импульс шаров до удара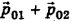 
равен суммарному импульсу шаров после удара 
:
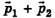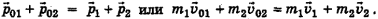
Абсолютно неупругим называется удар, при котором механическая энергия частично или полностью переходит во внутреннюю энергию соударяющихся тел. При этом кинетическая энергия со всем не превращается в потенциальную энергию упругой деформации, так как между телами не действуют силы упругости. При абсолютно неупругом ударе замкнутой системы тел закон сохранения механической энергии не выполняется, а выполняется только закон сохранения импульса. В результате такого удара тела движутся вместе в одном направлении с одинаковой скоростью, если после удара сохранилась часть бывшей у них до удара кинетической энергии, или покоятся, если их кинетическая энергия полностью превратилась во внутреннюю.
Рассмотрим абсолютно неупругий удар двух шаров массам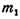и и 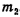, которые до удара двигались со скоростями 
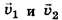а после удара приобрели скорость 
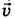(рис. 15-9).
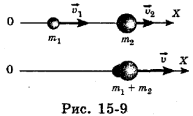
Пусть шары составляют замкнутую систему. По закону сохранения импульса суммарный импульс шаров до удара равен их суммарному импульсу после удара: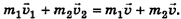 
Отсюда скорость шаров после удара
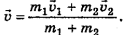
Для получения модуля скорости нужно спроецировать импульсы тел на выбранное направление (лучше сонаправить ось ОХ с направлением одного из импульсов) и перед импульсом, направленным противоположно, поставить «минус».
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:
