Пример решения задачи №47.
Тело массой m вращается по окружности в горизонтальной плоскости, будучи подвешенным на нити (рис. 11-4). Такая система тел называется коническим маятником.
Решение:
Очевидно, что на тело действуют только две силы: сила тяжести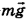 
и сила натяжения нити 
. Сила тяжести направлена, как всегда, вертикально вниз, а сила натяжения -вдоль нити к точке подвеса. При этом длины векторов 
должны быть таковы, чтоб их векторная сумма, т. е. диагональ параллелограмма, построенного на этих силах как на сторонах, была направлена по радиусу к центру окружности, по которой движется тело. Эта равнодействующая и есть центростремительная сила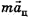 
. Таким образом, 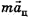не третья сила, а просто векторная сумма двух реальных сил, действующих на данное тело. Тогда второй закон Ньютона в векторной форме примет вид 
.
Чтобы написать второй закон Ньютона в скалярном виде, нужно записать соотношение между длинами векторов 
. Если известен какой-нибудь угол, например а при вершине конического маятника, то такой же угол (что несложно доказать) имеется и в прямоугольном треугольнике, катетами которого являются векторы 
. Тогда второй закон Ньютона для модулей сил примет вид 
.
Вообще хочется дать следующий совет. Если на вашем чертеже есть прямоугольный треугольник и в нем фигурирует какой-то угол а (дан или спрашивается, или нужен в процессе решения), то без тригонометрических функций никак не обойтись. Если на вашем чертеже получился треугольник, образованный векторами сил или скоростей, или просто какими-либо отрезками, длины которых известны или нужны по ходу решения задачи, и в этом треугольнике есть известный или необходимый для решения угол а, то в этом случае без теоремы косинусов не обойтись. Если треугольник прямоугольный, но никакие углы в нем не даны и не требуются, то, как правило, приходится применять теорему Пифагора.
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:
