Оглавление:





Тело бесконечных размеров. Всесторонне неограниченное тело
- Система координат x, y, r связана с объектом, размеры которого не ограничены ни в каком направлении. Приведите распределение температуры к точке времени. Поэтому предполагается, что поверхность с постоянной температурой является плоскостью, параллельной плоскости Y-r, а физические константы X, c и p равны constant. It необходимо изучить, как это начальное распределение температуры изменяется со временем. а) Математическая постановка задачи. Из — за того, что объекты во всех направлениях расширяются бесконечно, состояние поверхности исчезает, остаются только дифференциальные уравнения Начальное состояние. Решение с использованием интеграла Фурье.
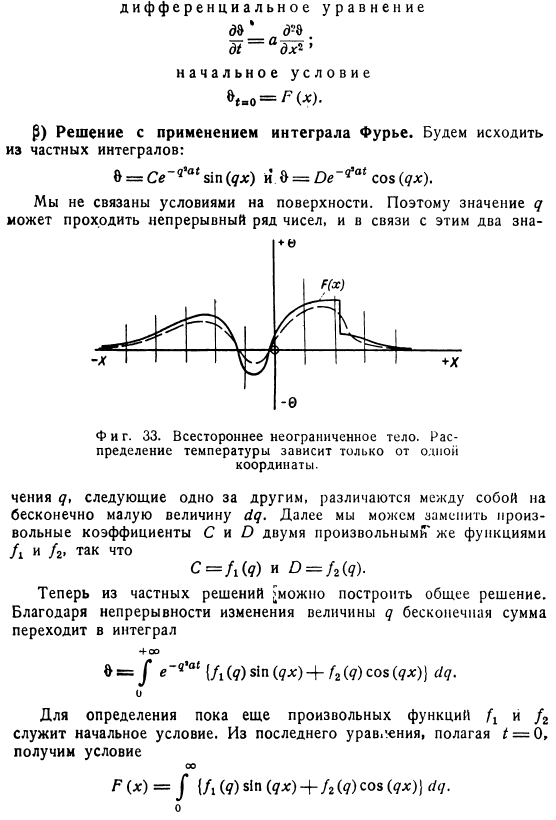
Начните с определенного интеграла. Он не связан состоянием поверхности. Таким образом, значение q может проходить через ряд последовательных чисел, и в этом отношении、 Рисунок 33.Комплексные неограниченные учреждения. Распределение температуры зависит только от 1 координаты. Затем замените любые коэффициенты C и O на 2 произвольные функции D и / 2.、 Вы можете построить универсальное решение из конкретного решения. При непрерывности изменения количества бесконечная сумма равна По-прежнему используйте начальное условие для определения любой функции и/ 2.
При какой скорости для условий задачи 11-3 охлаждающего воздуха влиянием свободной конвекции на перенос тепла можно пренебречь? Людмила Фирмаль
Получаем условие из последнего уравнения, которое устанавливает / = 0 Формула для интеграла Фурье(20) может быть: Для того, чтобы оба уравнения, определяющие P (x), соответствовали、 Поэтому уравнение температурного поля принимает вид: Для функции P, если этот двойной Интеграл фактически выполняется, величины и$не включаются в окончательный result. It ясно, что этот конечный результат будет только a, I и X функциями. В заключение, формула (36) показывает, что функция P (x) является интегралом Фурье (стр. 61) применима только в том случае, если условия применения выполняются, во-первых, неограниченным увеличением x, 4-CO Я хочу сделать его нулевым, чтобы y P (x) IX оставался нулем.
Из-за этого ограничения формула (36) теряет большую часть своей практической значимости. Однако есть и другой более широкий путь. s) решение с использованием закона ошибки Гаусса. Если данная функция P (x) не удовлетворяет приведенным выше условиям, то есть она остается бесконечной и конечной, или она не стремится к нулю так быстро, что интеграл остается конечным, то рассматриваемый путь не ведет к goal. In в связи с этим напомним, что дифференциальные уравнения также имеют некоторые другие интегралы(см. группу 44). Гауссовские правила распределения ошибок.
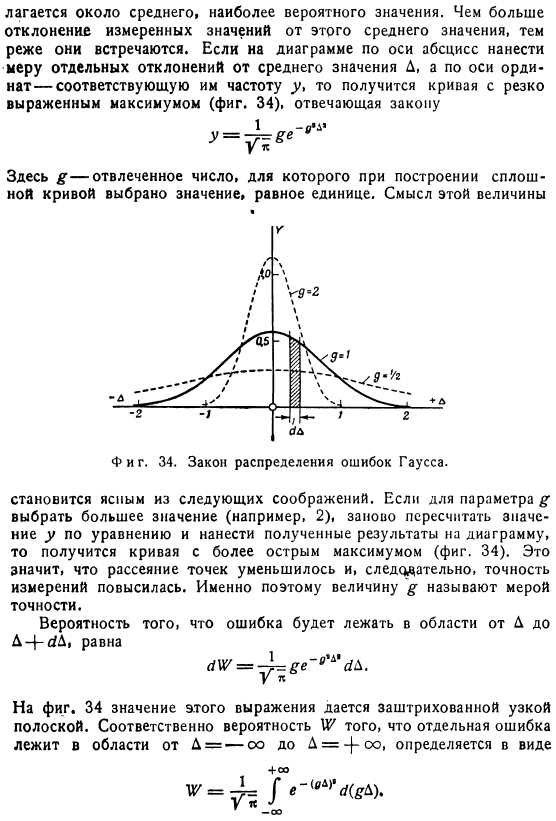
Смысл соотношения, представленного этой функцией, наиболее ясен при сравнении ее с законами теории вероятностей, в частности с теорией ошибок. Если у вас есть большое количество измерений, большинство данных расположено близко к среднему и является наиболее вероятным значением. Чем больше отклонение показаний прибора от этого среднего значения, тем реже они возникают. При проведении измерений индивидуальных отклонений от средних значений D вдоль абсциссы фигуры и соответствующих им частот y вдоль продольной оси получается кривая с выраженным максимальным значением, соответствующим закону (рис. 34).) Где & — абстрактное число, и в его структуре、 Тоже фигура.
Гауссовские правила распределения ошибок. Это ясно из следующих соображений: если вы выберете большое значение для параметра% (например, 2), пересчитаете значение y в соответствии с уравнением и примените результат к фигуре, вы получите кривую с более резким максимальным значением (рисунок 34).Это означает, что точность измерения улучшилась, так как рассеяние точек уменьшилось. Вот почему значение$называется мерой точности. Вероятность того, что ошибка находится в области от D до D4-s? Д » — К. Рисунок 1 34 значение этого выражения обозначено тонкой заштрихованной полосой.
- Аналогично, вероятность Y/, где единичная ошибка находится в области D = — °C до D = — | — oo, определяется в виде+ 00. Но как вы знаете、 Итак, C / = 1.Этот результат может быть получен непосредственно из понятия вероятности бесконечно больших областей ошибок без вычисления. Приведенные выше рассуждения включали в себя 2 результата, которые были особенно significant. As параметры увеличиваются, кривые становятся круче, а по мере уменьшения параметров они становятся более плоскими.
Однако площадь под кривой всегда остается постоянной, поэтому она не зависит от величины Если вершина кривой находится не на самой оси y, а в ординате, соответствующей D = D0, то другими словами, если начало координат сдвинуто»по уравнению D’ — D -: To», то закон распределения ошибок Гаусса называется формулой Частный Интеграл уравнения теплопроводности. Теперь вернемся к конкретному интегралу Сходство гауссовского закона распределения ошибок с этим решением поразительно. Значение коэффициента с описано ниже. Сделайте рассматриваемый объект бесконечно большим в некоторой точке(обозначьте его распределением температуры, удовлетворяющим уравнению) (Сплошная кривая на рис. 35).
Теплопроводность вычисляется в предположении, что тепло вследствие теплопроводности распространяется радиально от проволоки к трубке. Людмила Фирмаль
В этом случае последующее распределение может быть получено из этого distribution. To для этого замените время на большее значение, например/ 2 (кривая пунктирной линии на рисунке 35).Вы можете задать следующий вопрос: какое распределение этой температуры могло возникнуть из предыдущей? Уменьшение, то есть увеличение 1/|/, приводит к тому, что кривая становится круче и в конечном итоге сжимается до бесконечно узкой полосы шириной dx(пунктирная кривая на рис.35).Поскольку область под кривой должна оставаться конечной, легко увидеть, что ордината в этом месте будет бесконечно большой.
Теперь вычислите количество тепла, содержащегося в бесконечно длинной призме, вырезанной из объекта, параллельного оси X. Поперечное сечение призмы составляет 1us1g. Интегрирование уравнений Величина C представляет собой площадь между кривой температуры и осью абсцисс и измеряется в градусах * м. шкала, соответствующая величине cp, представляет собой количество тепла в призме с поперечным сечением, равным 1. обратите внимание, что в направлении оси y и оси r нет разницы температур, поэтому рассматриваемое количество тепла не должно зависеть от/.Следовательно, значение С должно быть постоянным и с физической точки зрения. Решение проблемы.
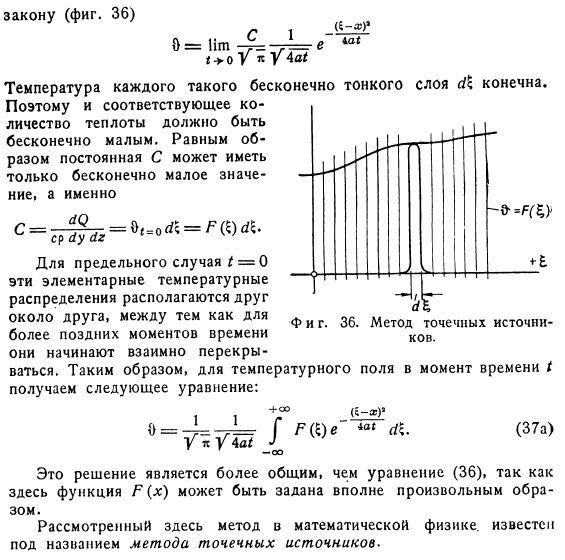
Здесь Напомним, что первый проход(p) не приходит к цели, если начальное распределение не позволяет представить x в виде интеграла Фурье. Однако, это начальное распределение может быть выражено как сумма отдельных дистрибутивов, и каждый распределение следует закону (рис. 36). Температура таких бесконечно тонких слоев конечна. Поэтому соответствующее количество тепла должно быть минимальным. Примерно равны Значение, которое константа C может иметь в то время, является c = ^ = b = o*=’? Если/ = 0, то эти основные распределения температуры располагаются рядом друг с другом, но в более поздние времена Тоже фигура.
Метод точечного источника. Они начинают перекрывать друг друга Перейдем поэтому к температурному полю времени I Получается следующее уравнение: Здесь функция P (x) может быть задана полностью любым способом, поэтому это решение является более общим, чем выражение (36).
Смотрите также:

