


Смотрите также:
- Теперь рассмотрим ламинарное течение пограничного слоя. Применяя уравнение Навье-Стокса к этой задаче, вы можете видеть, что некоторые из этих срезов пренебрежимо малы. Это верно только в том случае, если толщина пограничного слоя мала по сравнению с расстоянием от передней кромки и число Рейнольдсов велико. При малом числе Рейнольдса течение не предполагается, если область, где важна вязкость, простирается относительно далеко от границ тела (если есть примеры). Числа находят теорию Как довести его до крайности при ползании и жидкость.
Теория предполагает наличие скольжения жидкости по поверхности тела, поэтому полученные на ее основе результаты не совпадают с фактическим рисунком течения слоев жидкости вблизи поверхности тела. surface. In в этом слое скорость жидкости изменяется на величину, равную нулю у самой поверхности, и вязкостью здесь пренебрегать нельзя. Ч. Помните, что, как указано в. 8, это несоответствие истинному физическому образу особенно заметно при расчете сопротивления, а в теории идеальной жидкости обычно дает неверные результаты. Здесь рассмотрим упрощение, которое может быть достигнуто путем применения уравнения движения к 2-мерному, стационарному, ламинарному пограничному слою несжимаемой жидкости.
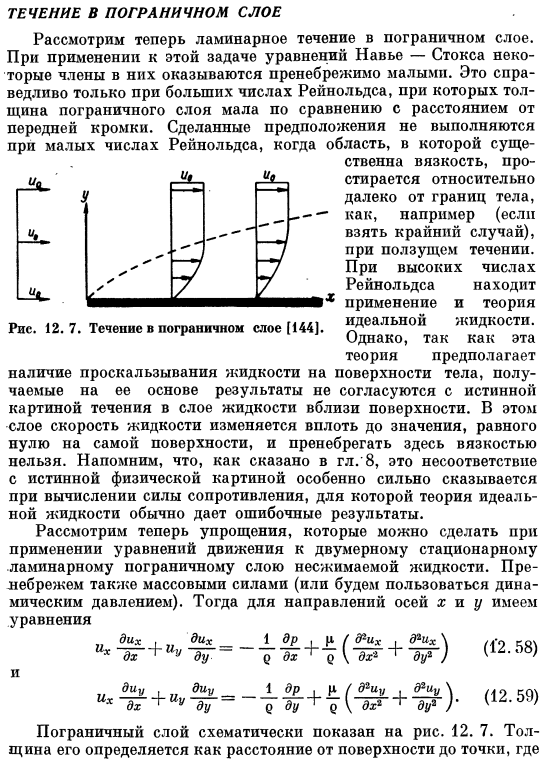
Игнорируйте также массовую силу (или используйте динамическое давление).Тогда есть уравнение для направления оси хны Да.-» Пограничный слой схематично показан на рисунке. 12. 7.Толщина определяется как расстояние от поверхности до U. Скорость достигает 0,99 и 0 (а 0-это значение скорости на поверхности, которое дает теория идеальной жидкости) x. Пограничный слой примыкает к твердой поверхности и считается очень тонким. thin.
Прандтль впервые показал[128, 129], что поперечная составляющая скорости uy очень мала по сравнению с продольной, а дифференциальная Это здорово по сравнению с другими приложениями. Это потому, что члены Порядок («7^») один и тот же, и оба они сопоставимы с»•. Руки, значение может быть проигнорировано сравнением Формула (12. 58) с другими участниками. Аналогичный анализ проводится в уравнении (12. 59), показывает, что все члены, включая скорость u и ее производную, малы. Это приводит к тому, что их практически нет conclusion. In другими словами, давление От поверхности тела до границ хосписного слоя немного мем. Этот результат очень важен.
Это связано с тем, что изменения давления, зависящие от координаты x, можно найти, рассматривая поток за пределами потенциала пограничного слоя. -В пограничном слое она может рассматриваться как заданная независимая от г Задача состоит из уравнений движения вдоль оси x и уравнения неразрывности(12. 44) стало совместным решением. С Это известно из решения вопроса о невязкой путем Кроме того, поскольку мы знаем, что если y = 0, то= uy = 0, а если y = b, то»u0, этих 2 уравнений достаточно, чтобы найти те и 2 неизвестных U. если x отсчитывается вдоль поверхности, а y перпендикулярно ей, можно использовать то же уравнение для границ кривой, где радиус кривизны больше 6.
Течет по плоской плите для потоков, проходящих через плоскую пластину, уравнение (12. 60.) По тому, что = 0, Ох, можно еще больше упростить так как U0-константа. Решение, которое дает им и ламинарный поток yi 1. используются и другие определения толщины пограничного слоя. (Заметьте, Пеле.)Движений функций x и y, которые были впервые приобретены Блазиусом[9] и усовершенствованы Хауартом[68].Уравнение (12. 60) и (12. 44) значительно проще уравнений в общем случае, но все же их детерминизм связан с математическими трудностями. Я объясню общее решение, не вдаваясь в детали. Одновременные уравнения(12.60) и(12. 44), функция потока позволяет свести к одному уравнению в частных производных.
- Функция тока определяется таким образом, что выполняется уравнение неразрывности несжимаемой жидкости. Это утверждение является формулой(12. 44) (12. 61) и (12. 62) проверяется путем прямого присвоения. Их ценности и ценности(12. 61) и (12. 62) против формулы (12. 60) замещение、 doodhdu dhu2 du’L (12.63) это нелинейное уравнение в частных производных 3-го порядка φ должно быть решено при указанных выше граничных условиях. (12. 63) решение дифференциальных уравнений вида не может быть получено с помощью обычных математических methods.
Как правило, это требует выбора, основанного на значительных физических и математических intuition. In в данном случае решение связано с тем, что профили скоростей в разных точках пластины одинаковы. Этот вывод можно считать основанным на физической интуиции*.Таким образом, скорость в любой точке представляется одной и той же функцией отношения〜.Толщина пограничного слоя b зависит от x, но увеличивается медленнее, чем первая степень X. In другие решения уравнения Навье-Стокса, не описанные здесь, мы можем предположить, что b является proportional. So предположим, что они являются функцией-y = (12. Шестьдесят четыре) 1.
Выводы о подобии профилей скоростей могут быть получены с помощью стандартного метода размерного анализа. 14 (см. также[14]).Поэтому нельзя согласиться с утверждением, что этот вывод основан на физической интуиции. (Примечание, trans) Формула (12. 63) пишется о φ, поэтому необходимо знать отношение между φ и ними. Формула (12. 61). если вы возьмете Φ= 0 на линии потока, проходящей через x = 0 и y = 0, вы можете написать следующее о точке x: (12. Шестьдесят пять) Да. Формула (12. 61) вы бы выглядели так: (12. Шестьдесят шесть) Формула (12. 67) заменить формулой(12. 63) становится обыкновенным дифференциальным уравнением х. приведенная выше простая формула(12. 64) и 12.
Вместо формулы (12. 63) значение, используемое для упрощения обычно описывается в виде следующей безразмерной переменной. (12.68) II Д. (12.69) Где m]можно рассматривать как безразмерную координату, а/(μ) можно рассматривать как безразмерную функцию тока. Отношения (12. 68) и (12. 69) называется преобразованием подобия. После длительного расчета, согласно правилам расчета частной производной 2, Формула(12. 63) преобразуется следующим образом: / (П)^-+ 2 ^ = 0(12.70) 1 в оригинале формула(12. 67) вывод основан на чрезмерных предположениях. При переводе текст будет меняться соответствующим образом. (Прим, Персе.) 8 краткое изложение этих правил является[113], pp. It дается в 209-213 гг.
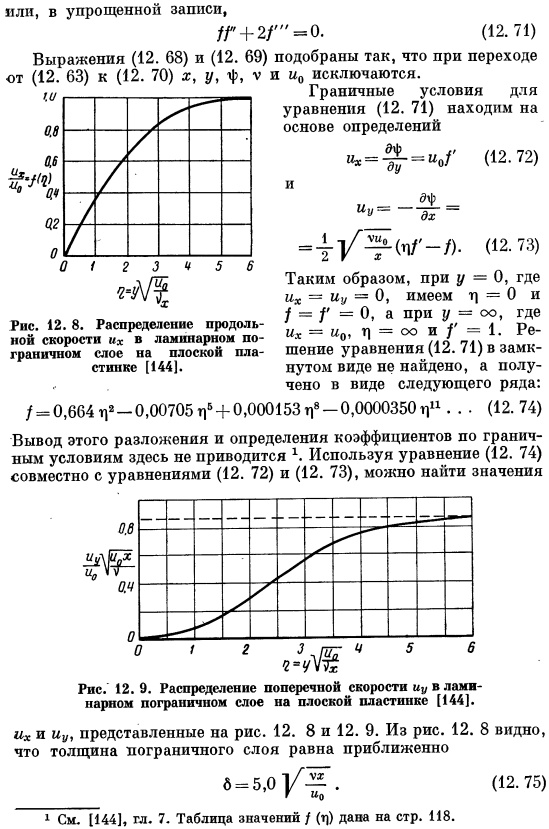
Формула (12. 68) и (12. 69) из (12. 63) из (12. 70)я, Г, ф, В 12. 8.Распределение продольной скорости в ламинарном пограничном слое на плоской пластине[144]. Выбрано для исключения u0 во время перехода. Уравнение (12. 71) граничные условия найдены на основе определения «* = + =» / ’(12-72)и еще = г•/ α -/). 12-7 Итак, если y = 0, если u = uy = 0, то z = 0 и / = f ’= 0, а если y = oo, то u = u0,= = oo и f’ = 1. 12. 71) не будет выплачиваться в закрытом виде, но получит в виде следующей серии. / = 0.664 С2-0.00705 ХБ +0.000153 С8 −0000350 т / н 。 。 (12. 74) вывод этого расширения и определение коэффициентов из граничных условий здесь x не даются. Формула 12.
Формула (12. 72) и (12. 73) может быть использован для поиска значения. Рис. 12.9.Распределение поперечной скорости yi в ламинарном пограничном слое на плоской пластине[144]. Их и yiw, показанных на рисунке. 12. 8 и 12. 12.8-это приблизительно толщина пограничного слоя 6 = 5.01/^. (12.75) ’^0 См. 1 [144]. 7. таблица значений f (q) находится на стр.
Смотрите также:
| Ламинарное движение в кольцевом зазоре | Сопротивление при обтекании плоской пластинки |
| Движение идеальной жидкости | Течение на входном участке трубы |
