




- Внутренняя поверхность промышленной трубы не обязательно гидравлически гладкая. Таким образом, график коэффициента сопротивления (рис.15. 1) показывает кривую относительной шероховатости в различной степени. На диаграмме 15. 1 основана на данных многих исследователей по лечению Мууди [116]. Это выражение неточно. Потому что понятие «гидравлически гладкая труба» определяется только применительно к данной проточной ситуации. 13. Форма кривых грубой трубы отличается от полученной методом для труб искусственной шероховатости(стенки трубы были склеены песком) — см. Рисунок 13.9.
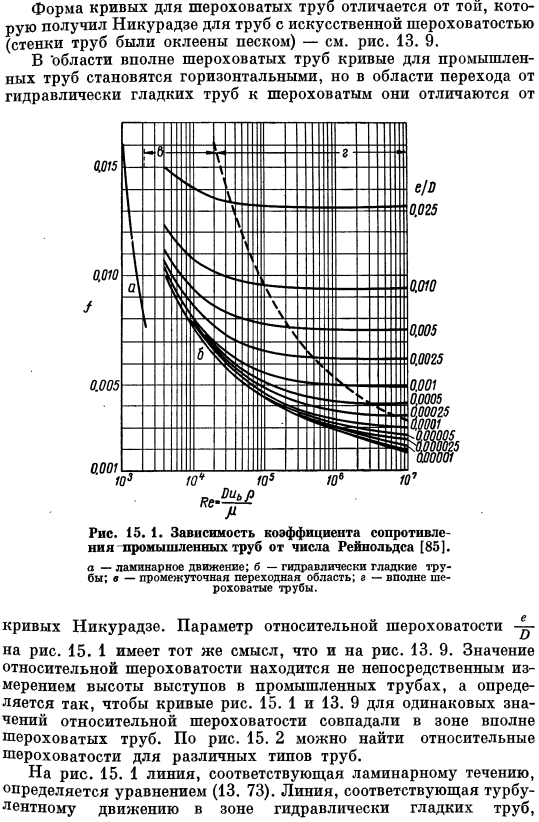
В области полностью шероховатых труб, кривые промышленных труб нивелируются, но при переходе от гидравлически гладких труб к грубым、 Рис.15. 1.Зависимость коэффициента сопротивления промышленных труб от числа Рейнольдса[85]. а-ламинарное движение; б-гидравлически гладкая труба; в-промежуточная переходная область; а-очень шероховатая труба. Кривая никлаза. Рисунок параметр относительной шероховатости 15. 1 означает то же, что и Рисунок 1. 13. 9.Величина относительной шероховатости не является прямым измерением высоты выступа промышленной трубы, но кривая на рисунке 13 показывает ту же шероховатость, что и относительная шероховатость 15. 1 и 13. 9, совершенно соответствуют в зоне грубых труб.
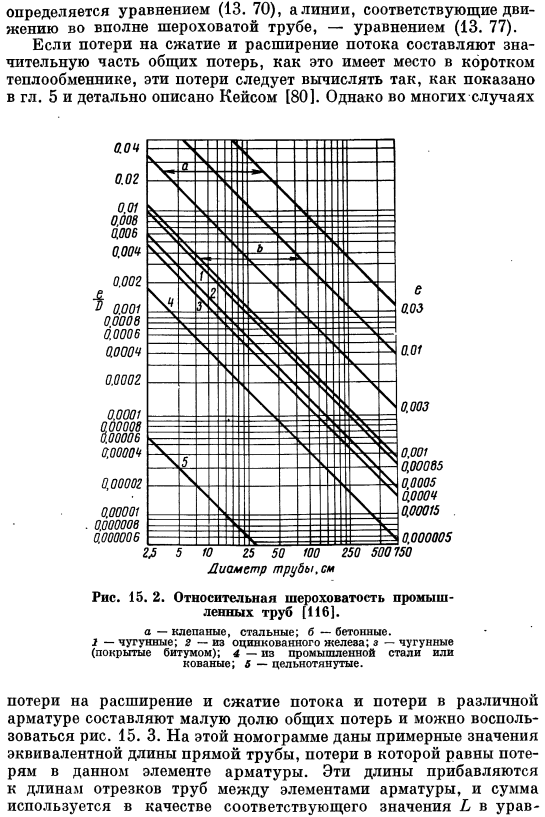
Согласно рисункам 15. 2 вы можете найти относительную шероховатость различных типов труб. Рис. 15.1 ряд, соответствующий ламинарному течению, представляет собой формулу(13. 73).Линия, соответствующая турбулентному движению в зоне гидравлически гладкой трубы, вычисляется по формуле (13. 70) определяется уравнением (13. 77). Если, как и в случае коротких теплообменников, потери на сжатие и расширение составляют значительную часть общих потерь, то эти потери следует рассчитать, как показано в разделе. 5, случай[80] описан подробно. Однако во многих случаях Рис.15. 2.Относительная шероховатость промышленных труб[116]. а-заклепки стальные; б-бетон.
Потеря расширения и сжатия потока и потеря различных фитингов составляют небольшую часть общей потери. Вы можете использовать диаграммы. 15. 3.Эта номограмма дает приблизительное значение эквивалентной длины прямой трубы. Эта потеря равна потере элемента ножки клапана. Эти длины суммируются с длинами отрезков трубы между армирующими элементами, сумма которых используется в качестве соответствующего значения формулы b. p. d. Давайте начнем. Мнение (15.2). в то же время длина значения 2 и Teach равны, поэтому эти термины можно опустить.
В следующем примере показано более полное применение этих методов. Пример 15.1 Вода при температуре 16°с направляется по трубопроводу в открытый резервуар с расходом 380 литров из резервуара! От бака к насосу протягивается стальная труба диаметром 78 мм, а для бака, установленного над ним от насоса, используется стальная труба диаметром 053 мм. Длина трубы и фитинги показаны на рисунке. 15. 4.Рассчитайте мощность, которую насос будет потреблять (если она составляет 70%). Решение проблем В этом случае потери давления Dp равны нулю, а Di ^равен нулю, а Dt = 5.1 м. Формула (4.27) выглядит так: 9.8 * 5.1 + л / 4-0.
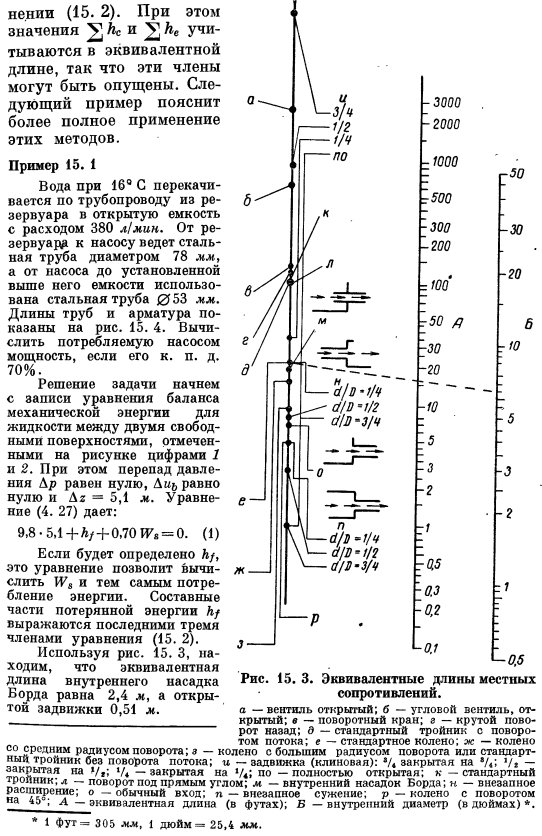
Если L / определяется, то это уравнение может вычислить\ U8 и тем самым рассчитать потребление энергии. Составной частью потерянной энергии K / является формула (15. 2) представлен последними 3 членами. С рисом. 15. 3, эквивалентная длина внутреннего сопла платы составляет 2,4 м, открытая задвижка-0,51 м. Т50 Д −100. −300 −200. ^ 1000 — 3000. Двухтысячный ^ −0.5 Рис.15. 3.Эквивалентная длина локального сопротивления. а-открыть вентиль; б-открыть угловой вентиль; в-повернуть кран; а-крутой спуск.
Стандартный тройник с вращением потока D; e-стандартное колено; G-колено со средним радиусом поворота; a-колено с большим радиусом поворота или стандартным TR°YNIK без изменения потока; и-задвижка (клин): * / •/ ; ’/»-* /、; ‘/ 4-* / он закрыт в 4. по-моему, он полностью открыт. k-стандартный Тропик. l-поворот на прямой угол; m-внутренняя доска сопла. Н-внезапное со /?РЕН? e; ° ’ нормальный вход; n-внезапное сужение; P-колено на повороте; d-эквивалентная длина (в футах). B-внутренний диаметр (дюйм)*. * 1 фут= 305 мм, 1 дюйм » 25,4 мм. Таким образом, эквивалентная длина первого участка трубопровода равна 2.4 4-6 + 0.51 + 9 = 17,9 м.
- Он также вычисляет следующие значения для раздела I. 380-10 — » −1000.= 633 кг / с. 60. 6.33 = 47.7.10 — ^ — ^-1133 1000-1. 33-78-10-3 1.05•10 ″ 3 а-внутренняя насадка. б-открыть клапан; в-насос; а-стандартный тройник; д-вен-Тиль закрыть. 15.3 поиск по рисунку: — = 0, 0006 согласно рисунку 15. Коэффициент сопротивления 1 / = 0.0052.So для участка I потери равны 2/24 _ 2-0,0052.17,9-1.33 *-Дж / ^ —— 78-10-3 Аналогичный расчет выполняется при определении потерь II. Трубопровод. Для чая, b = 4 m. In случай потери расширения на входе в верхний бак представлен на рисунке 15. 3—-= 0, поэтому нет подходящей точки. Но вы можете видеть из формулы в примере 5 (5) до 2.
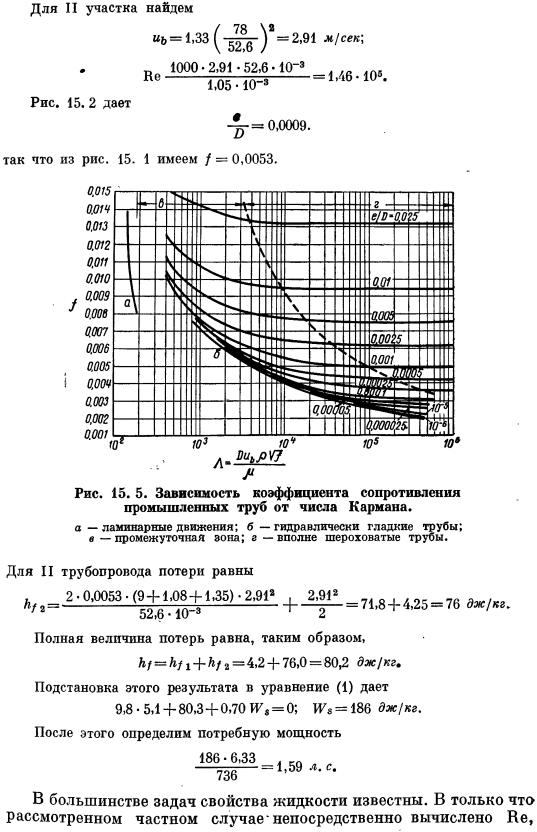
Рисунок 15.2 давать (U-2,91 м / с} 1000•2.91•52.6•10 ″ 8 1Л6. 105 б = 1.33 № 1,05 * ю » 8 — ^- =0,0009. 15 из рисунка. 1 = 0,0053. Рис.15. 5.Зависимость коэффициента сопротивления промышленных труб от количества карманов. а-ламинарное движение; б-гидравлически гладкая труба; в-Средняя зона. Г-довольно грубая труба. В случае трубопровода II потери равны Б 2•0.0053•(94-1.084-1.35)•2.918、 ————— ой е. 4Л-3Г О 042 = 71.84-4.25 = 76 Дж / кг.
Таким образом, общая потеря составляет А / = Л/! 4-л/ 2 = 4.2 4-76.0 = 80 ^ Дж / кг Если присвоить этот результат выражению (1)、 9.8-5.14-80.34-0.70 W,= 0; W «= 186 Дж / кг. Затем определите необходимую мощность 186-6. 33. Семьсот тридцать шесть В большинств применениях, жидкие свойства known. In в конкретном рассматриваемом случае он рассчитывается непосредственно Рисунок из 15. Значение 1 / получается и выражение (15. 1) определяется величина потерь от/до.
С другой стороны, если вместо скорости установлен выход насоса, то для определения скорости (т. е. расхода) необходимо знать b, чтобы определить как число Рейнольдса, так и коэффициент сопротивления, поэтому следует использовать метод непрерывного приближения. Рисунок 15.to решить задачу скорость неизвестна (то есть задана в/).Представьте, что вам не нужно знать скорость, чтобы определить abscissa. To для этого введите переменную A следующим образом: (15.3) по словам Дани пик. 15. Значение 1 А и соответствующее/легко вычислить. Рис.15. 5 показан график зависимости/от L. В следующем примере показано его использование.
Пример 15.2 . Горячая вода при температуре 44°с вытекает из резервуара, где уровень не изменяется, по стальной трубе диаметром 52 мм. Выход из трубы расположен на 12 м ниже уровня в резервуаре. Эквивалентная длина трубопровода 45.k. рассчитайте расход с помощью l! Минута. Если вы получаете уровень жидкости в баке во входном сечении и конец трубы в выходном сечении, уравнение равновесия механической энергии уменьшается следующим образом: Ди? М * + −2 ^-+ Л / = 0( » Или входная скорость равна нулю, Дг = −12.to быть、 −9、§ 12±^-(1 + ^-)= 0 (2) Уравнение (2) показывает, что относительное значение кинетической энергии увеличивается с уменьшением.
И, следовательно, и использовать фигуру, чтобы найти&. 15. 5.Расчет Он> Из рисунка 15.5 при = 0.0009 / = 0.0049 В предыдущем расчете A / было равно 118, Как мы можем получить из уравнения (1), которое пренебрегает кинетической энергией. Если этот термин важен, вы можете исправить его позже. Выражение (2) принимает вид: ■ «118+» g(1 + 4•0.0049 * 45 \ l. 52 * 10″ 8 Y » 0、 И напоследок −118 +(1-4-16. 9) равно 0 Вы можете использовать это значение B уравнения (1) для вычисления нового значения A /и получения нового значения He. Однако значение параметра/не изменяется, поскольку последнее значение изменяется только несколько раз.
So, b = 3,63 м / с-правильный результат, а расход равен 3.63•0.785•522•10-•60•108 = 452 л / мин Это не может быть названо карманным номером выражения. Если тогда, в зависимости от сюжета-m = — ^(Be)//), как Формула (13. 70) показывает, что в области гидравлически гладких труб получается прямая линия. Такой график дан, например, Роузом [138].
Смотрите также:
| Метод Релея | Течение в параллельно соединенных трубах |
| Баланс механической энергии | Течение в некруглых трубах |
