
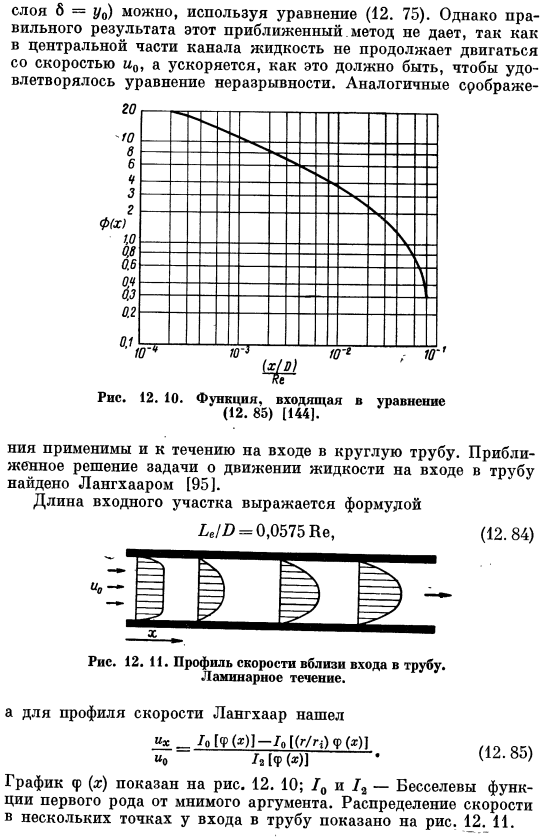



- Развитие профиля скорости было показано на рисунке. 8.6. Для бесконечно широких прямоугольных каналов. Пограничный слой появляется на верхней и нижней стенках. Положение в этом случае аналогично обтеканию плоской пластины уравнением (12. 75) можно использовать для оценки длины входного сечения (то есть расстояния до точки, где толщина пограничного слоя будет равна 6 = y0). Однако этот метод аппроксимации не обеспечивает правильного result. In в средней части канала жидкость не продолжает двигаться со скоростью u0, а ускоряется, поэтому уравнение неразрывности удовлетворяется. Аналогичная сробра- 12. 10.Формула (12. Функция, которая появляется на 85) (144].
Уравнение может быть применено к потоку на входе в круговой канал. pipe. An приближенное решение задач движения жидкости на входе в трубу было найдено Лангхааром [95]. Длина входного участка представлена следующей формулой (12. 84.) Для профиля скорости, «немецкая длинношерстная» нашли Их _ — сайта mphc*)]- 7О ((г / н) ф (*)] МО [Ф(*)] (12.85) График f (x) показан на рисунке. 12.10; функция Бесселя для 10 и-1 рода мнимых аргументов. На рисунке показано распределение скорости в нескольких точках входа в трубу. 12. I. Заключение Удобно перечислить типы задач, которые могут быть решены с использованием основных принципов гидродинамики, которые были изучены до сих пор.
Сохраненное уравнение в интегральном виде позволяет найти либо входные, либо выходные параметры процесса, если на входе и выходе известно достаточное количество других parameters. In в частности, уравнения равновесия импульса обеспечивают полезный способ изучения случая течения и других движений через диафрагму, когда эффект инерции велик. 2.Уравнения движения позволили найти решение изотермического стационарно-ламинарного течения несжимаемой жидкости на расстоянии от входа в канал. При тех же условиях получено решение ламинарного пограничного слоя на плоской пластине. 3.С другой стороны, проблемы, связанные с турбулентностью в трубах или в пограничном слое, не рассматривались.
При исследовании пограничного слоя не учитывалось образование потока и следа вблизи отрыва point. In при аналитическом исследовании этих задач были достигнуты определенные успехи, но основные методы их инженерного решения основаны на идее размерного анализа и важном использовании экспериментальных данных. Эти методы составляют содержание следующих нескольких глав книги. Задачи 12. 1.Формула (12. 5) смогите быть приложено к подаче в зазор.1. одна из его стенок движется с постоянной скоростью u0.
- В зависимости от y, u0 представляет скорость, указывая положительные и отрицательные значения, и результирующий профиль положительного u0. Этот тип течения называется Куетговским и играет важную роль в гидродинамической теории смазки. Если = 0, то это называется простым потоком Ку-Этта. Мы столкнулись с этим случаем, когда было введено понятие вязкости-см. диаграмму. 7.1 и уравнение (7.2). 12. 2.Не обращая внимания на ускорение пленки, находим формулу распределения скоростей в пленке, протекающей по вертикали plane. In в этом случае градиент давления в направлении движения отсутствует, но важна массовая сила (гравитация).Найдите также формулу толщины пленки по средней скорости. 12.
Формула (12. 35) найти временную зависимость положения плотностного шара е, вышедшего из стационарного состояния. Значение не при конечном (максимальном) значении скорости меньше 1.Какова формула конечной скорости? 12. 4.Потенциальный 2-D отток жидкости из большого резервуара выражается следующей формулой: вычерчивают линии течения и эквипотенциальные линии этого потока (то есть сети потоков) и определяют расположение стенок канала. 12. 5.Для 2-D потенциального потока вокруг идеализированной трубки Пито сеть потока определяется: X = -dd.1П / / 2_ / _2; Y = — Φ4-ags1& -> -. Нарисуйте линию потока для этого потока.
Для конкретного потока потенциал задается формулой Φ= xy. Какой формы должна быть твердая граница, определяющая этот поток? 12. 7.Течение вблизи сферы радиуса r0 определяется в сферических координатах по формуле φ= cos0 + u0 r cos0.Где 0-угловая координата Ди Ната (лат. Если 0 = 0 соответствует передней критической точке, найти направление скорости при r = — r0 и 0 = 30°. 12. 8.
Воздух при температуре 16°С и нормальном атмосферном давлении течет продольно вокруг плоской пластины со скоростью 9 м / с. какова толщина пограничного слоя на расстоянии 1 м от передней кромки? Также вычисляется сила сопротивления, действующая на первый метр пластины шириной 1 г. 6.
Смотрите также:
