Таблица производных, правила дифференцирования, производная обратной функции

Таблица производных

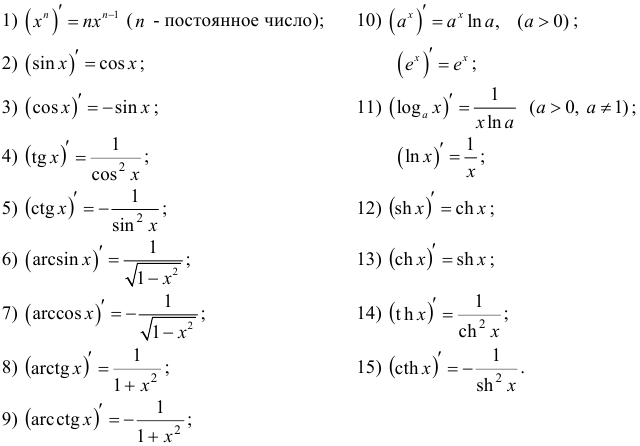
Правила дифференцирования

Если 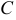— постоянная величина и функции 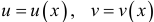имеют производные, то

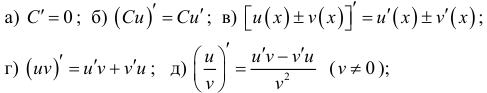
Производные показательно-степенных функций вычисляют по формуле

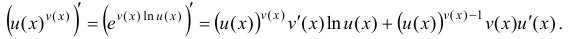
Производная второго порядка от функции 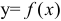определяется как 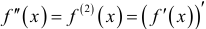. Аналогично определяются производные высших порядков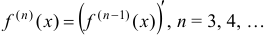

Дифференциал функции

Если приращение функции 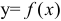от независимой переменной 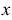может быть представлено в ви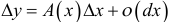де , где 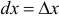, то главная линейная часть этого приращения называется дифференциалом функции 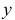: 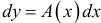. Для существования дифференциала функции 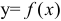необходимо и достаточно, чтобы существовала конечная производная 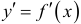, причем имеем 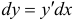. Последняя формула будет верна и в том случае, если переменная 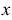является функцией от новой независимой переменной (свойство инвариантности первого дифференциала). Дифференциалы высших порядков от функции 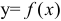последовательно определяются формулами 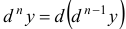, 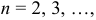где принято 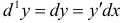. Если 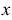— независимая переменная, то полагают 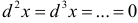. В этом случае справедливы формулы 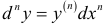и .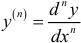

Производная обратной функции

Дифференцируемая функция 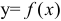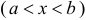с производной 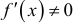имеет однозначную непрерывную обратную функцию 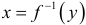, причем обратная функция также дифференцируема и справедлива формула .

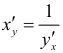На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:

Высшая математика краткий курс лекций для заочников

Возможно вам будут полезны эти страницы:

Непрерывность функции в точке

Производная. Механический и геометрический смысл производной

Производная функции, заданной параметрически

Производная функции, заданной в неявном виде