Оглавление:
Таблица основных неопределенных интегралов
Пользуясь тем, что интегрирование есть действие, обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул дифференциального исчисления (таблица дифференциалов) и использования свойств неопределенного интеграла.
Например, так как
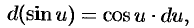
то
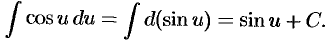
Вывод ряда формул таблицы будет дан при рассмотрении основных, методов интегрирования.
Интегралы в приводимой ниже таблице называются табличными. Их следует знать наизусть. В интегральном исчислении нет простых и универсальных правил отыскания первообразных от элементарных функций, как в дифференциальном исчислении. Методы нахождения первообразных (т. е. интегрирования функции) сводятся к указанию приемов, приводящих данный (искомый) интеграл к табличному. Следовательно, необходимо знать табличные интегралы и уметь их узнавать.
Отметим, что в таблице основных интегралов переменная интегрирования 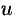 может обозначать как независимую переменную, так и функцию от независимой переменной (согласно свойству инвариантности формулы интегрирования).
может обозначать как независимую переменную, так и функцию от независимой переменной (согласно свойству инвариантности формулы интегрирования).
В справедливости приведенных ниже формул можно убедиться, взяв дифференциал правой части, который будет равен подынтегральному выражению в левой части формулы.
Докажем, например, справедливость формулы 2. Функция 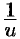 определена и непрерывна для всех значений
определена и непрерывна для всех значений 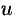 , отличных от нуля.
, отличных от нуля.
Если 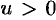 , то
, то 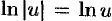 , тогда
, тогда 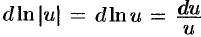 . Поэтому
. Поэтому 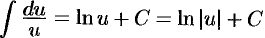 при
при 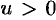 .
.
Если 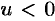 , то
, то 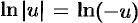 . Но
. Но 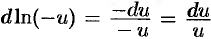 . Значит,
. Значит, 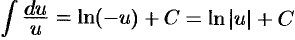 при
при 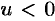 .
.
Итак, формула 2 верна.
Аналогично, проверим формулу 15:
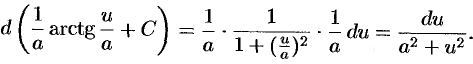
Таблица неопределенных интегралов
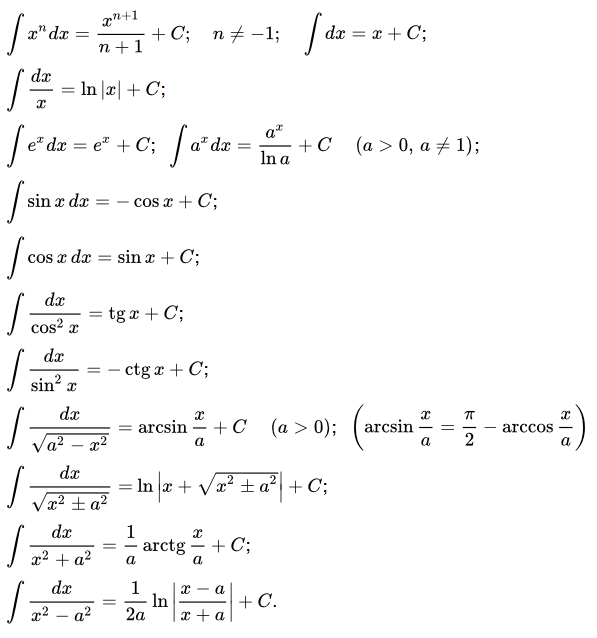
Таблица основных интегралов
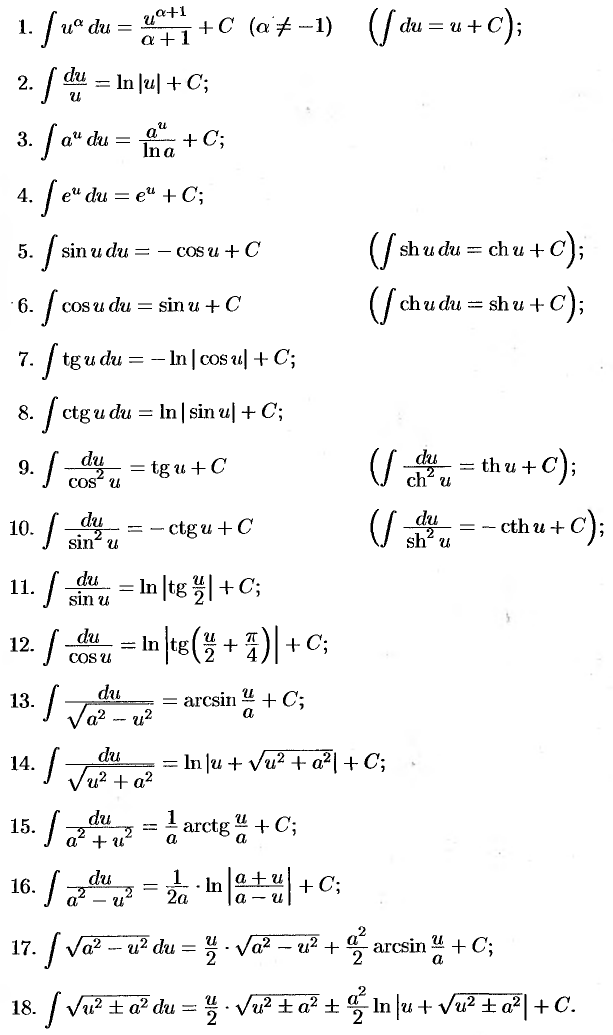
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Общая схема исследования функции и построения графика |
| Функции двух переменных |
| Функциональные ряды |
| Абсолютная и условная сходимости числовых рядов |

