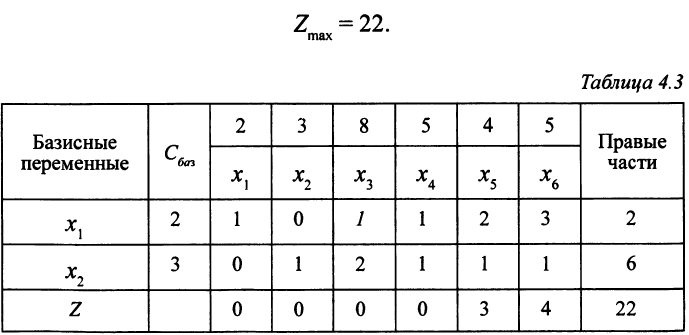
Пример №17.
В табл. 4.3 стоит оптимальное ОР, на котором целевая функция достигает своего максимума, — вектор 
= (2; 6; 0; 0; 0; 0);
Перейдем к новому ОР, заменив в первом уравнении базисную переменную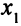 
на переменную 
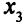(табл. 4.4).
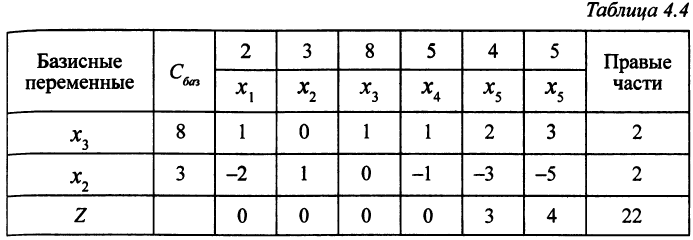
Оценки переменных и значение целевой функции, конечно, не изменились. ОР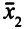 
= (0; 2; 2; 0; 0; 0) также оптимально.
Если теперь в первом уравнении заменить базисную переменную 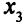переменной 
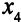, получится еще одно оптимальное ОР — вектор 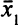= (0; 4; 0; 2; 0; 0).
Пусть некоторая ЗЛП имеет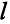 
оптимальных опорных решений:
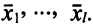
Докажем, что любой вектор
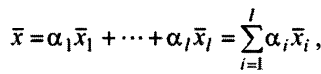
где
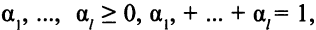
является допустимым и оптимальным решением этой ЗЛП.
Вектор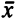 
называется выпуклой линейной комбинацией векторов 
.
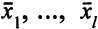Если 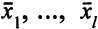— оптимальные решения, то они одновременно допустимы:
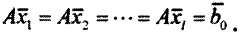
Тогда
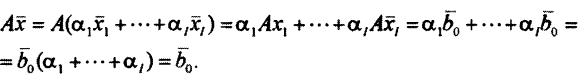
Кроме того,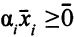 
в силу условия 
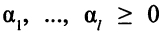. Вектор 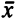— действительно допустимое решение. Далее, если 
=
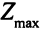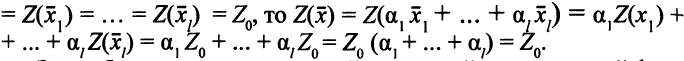
Здесь было использовано свойство линейности целевой функции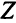 
.
Применительно к рассматриваемому примеру оптимальным решением задачи является всякий вектор
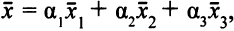
где
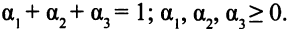
Пусть, например,
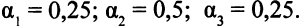
Этому набору значений коэффициентов линейной комбинации соответствует оптимальное решение задачи с такими значениями переменных (конечно, уже не опорное):
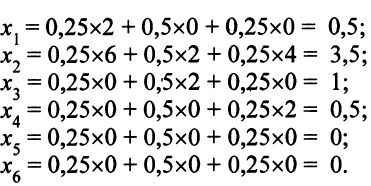
Понятие об альтернативных оптимальных решениях может оказаться полезным при анализе решений практических задач.
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
| Пример №15. Общий способ избавления от вырожденности |
| Пример №16. Решить ЗЛП |
| Пример №18. Для изготовления изделий требуется сырье трех видов |
| Пример №19. Решить симплекс-методом |
