Сжатие множества допустимых решений
Метод е-ограниченнй. При нахождении оптимального решения задачи МКЛП этим методом выбирается для максимизации только один из критериев, остальные критерии ограничиваются снизу некоторыми числами е; т.е. переводятся в условия-ограничения, тем самым сжимаютобластьдопустимых решений. Таким образом, вместо задачи МКЛП решается задача Л П: найти
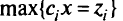
при ограничениях
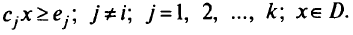
Однако пользователь сам определяет, какие критерии нужно перевести в ограничения и с какими значениями правых частей Например, неверный выбор 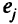 может привести к несовместной задаче линейного программирования. Решение принимается на основе анализа серии подобным образом построенных задач ЛП, т.е. процедура решения задачи МКЛП носит интерактивный характер.
может привести к несовместной задаче линейного программирования. Решение принимается на основе анализа серии подобным образом построенных задач ЛП, т.е. процедура решения задачи МКЛП носит интерактивный характер.
Анализ почти оптимальности — другой способ сжатия области допустимых решений. Процедура анализа эффективной точки выглядит так:
- Решить задачу ЛП со взвешенными суммами: найти
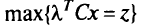 при ограничении
при ограничении 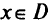 и определить величину
и определить величину 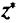 .
. - Выбрав некоторое
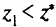 , решить задачу ЛП для сжатой области допустимых решений.
, решить задачу ЛП для сжатой области допустимых решений. - Вычислить все критериальные векторы
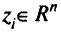 , соответствующие крайним точкам
, соответствующие крайним точкам 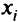 сжатой области.
сжатой области. - Выбрать точку
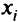 соответствующую самому предпочтительному вектору в качестве окончательного решения МКЛП.
соответствующую самому предпочтительному вектору в качестве окончательного решения МКЛП.
Трудности здесь могут возникнуть при нахождении всех альтернативных оптимумов для вычисления всех крайних точек.
В общем случае задачи МКЛП приводят к следующим взаимоисключающим и исчерпывающим ситуациям. Пусть 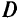 — множество допустимых решений,
— множество допустимых решений, 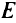 — эффективное множество, тогда:
— эффективное множество, тогда:

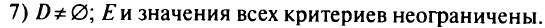
В любом случае надо найти исходную эффективную крайнюю точку. Для этого можно использовать методы: 1) взвешенных сумм; 2) взвешенных сумм с использованием подзадачи-теста; 3) лексикографической максимизации; 4) лексикографической максимизации с использованием подзадачи-теста; 5) Эккера-Куоды; 6) Бенсона.
В методе взвешенных сумм выбирается некоторое
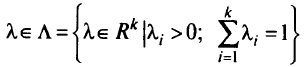
и решается задача
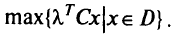
Если область допустимого решения  ограничена и
ограничена и 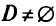 , то эффективная точка будет найдена. Если область
, то эффективная точка будет найдена. Если область  не ограничена, метод не гарантирует нахождения эффективной точки.
не ограничена, метод не гарантирует нахождения эффективной точки.
При использовании подзадачи-теста еще до нахождения максимума целевой функции проверяются крайние точки в процессе работы этого метода, что экономит время. При этом уменьшается вероятность неудачной реализации метода взвешенных сумм в случае неограниченной области  .
.
В процессе лексикографической максимизации применяется следующая процедура сжатия допустимых областей:
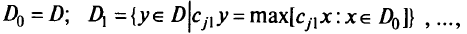
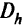 — область сжатия допустимой области после
— область сжатия допустимой области после 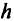 максимизаций,
максимизаций,
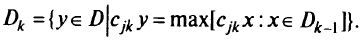
Процесс начинается с максимизации целевой функции 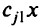 в области
в области 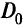 . Затем, ограничиваясь точками из
. Затем, ограничиваясь точками из 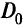 , максимизируем
, максимизируем 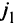 -й критерий и получаем область
-й критерий и получаем область 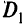 . В области
. В области 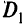 максимизируем второй критерий
максимизируем второй критерий 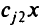 и, ограничиваясь точками из
и, ограничиваясь точками из 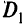 , максимизирующими
, максимизирующими 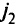 -й критерий, — получаем область
-й критерий, — получаем область 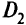 . Процесс продолжается до тех пор, пока не получим либо
. Процесс продолжается до тех пор, пока не получим либо 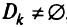 , либо, начиная с некоторого
, либо, начиная с некоторого
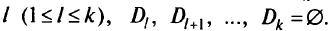
Последнее будет иметь место, если все остающиеся целевые функции не ограничены на 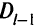 .
.
При использовании подзадачи-теста быстрее находится эффективная точка и метод улучшается при неограниченности на 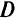 всех критериев. Подзадачу можно применять в начальной крайней точке и повторять проверку после каждого шага максимизации или проверить каждую крайнююточку. Метод не гарантирует от неудачи, если все критерии неограничены на
всех критериев. Подзадачу можно применять в начальной крайней точке и повторять проверку после каждого шага максимизации или проверить каждую крайнююточку. Метод не гарантирует от неудачи, если все критерии неограничены на 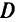 и
и 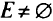 .
.
В методе Эккера-Куоды решается вспомогательная задача:
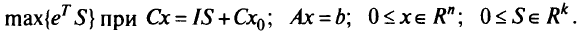
Если 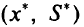 — оптимальное решение этой задачи, то
— оптимальное решение этой задачи, то 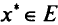 , и если целевая функция
, и если целевая функция 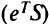 не ограничена сверху, то
не ограничена сверху, то 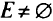 . При этом здесь нет гарантии, что обнаруженная эффективная точка будет точкой области
. При этом здесь нет гарантии, что обнаруженная эффективная точка будет точкой области 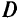 .
.
В методе Бенсона предлагается следующая процедура для определения исходной эффективной крайней точки:
Пусть 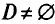 . Найти любую точку
. Найти любую точку
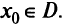
Решить задачу
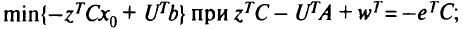
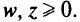
Если оптимального решения этой задачи не существует, то задача МКЛП не имеет эффективных точек. Если есть оптимальное решение
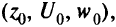
то переходим к шагу 3.
Положить
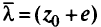
и решить задачу
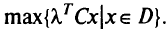
В результате найдем начальную эффективную крайнюю точку.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
| Многокритериальные задачи линейного программирования |
| Метод взвешенных сумм с точечным оцениванием весов |
| Минимальные значения критериев на множестве эффективных точек |
| Параметризация целевой функции |

