Оглавление:
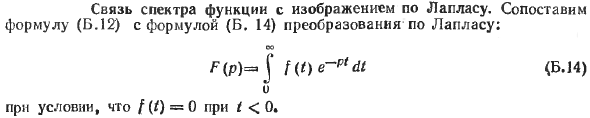


Связь спектра функции с изображением по Лапласу
Связь между спектром функции и изображением Лапласа. Сравните уравнение (B.12) с уравнением преобразования Лапласа (B. 14): 00 f (P) = J (B.N) 0, где f (t) = 0, если t <0.
- Если T <0, то заменить D /) = 0 и заменить p на / co, тогда
уравнение (B. 14) становится уравнением (B. 12). Людмила Фирмаль
Таким образом, спектральное уравнение для функции 6 (ω) можно получить из соответствующего уравнения на изображении Лапласа, подставив / ω для последнего p.
Пример 171. Используйте таблицу (см. Стр. 398), чтобы найти спектр G (ω) функции f (/) = e-®® *.
- Предположим, что f (/) = 0 равно / <0. (См. Стр. 398) Дается изображение функции Карсона (не Лапласа). Функция / (
Чтобы получить изображение по Лапласу, равному 0, на стр. Лаплас: «4-П». 4-П.
разделите изображение этой функции по Карсону Людмила Фирмаль
Замените п / к, чтобы получить спектр G ( co) =; G (u) — комплексное число, равное / fl, модуль которого G равен-; аргумент <rz; = arc tg -.A b -j- co2 a
Смотрите также:

