Оглавление:
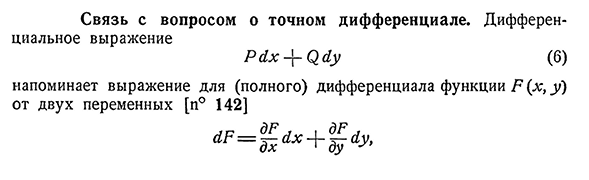





Связь с вопросом о точном дифференциале
- Связь с проблемой точной дифференциации. Дифференциальное выражение P y x (6)аналогично (полной) производной функции P(x, y) двух переменных[n°142] Р=К х+Д у АС>350]§4. Независимое условие криволинейного интеграла 269 Это определяется в (6) при размещении DX>(7) однако не все выражения в форме (6) являются
«точными производными», и не все выражения имеют «примитивные функции» P(x, y), и мы снова сталкиваемся с тем же условием (A) при определении того, является ли выражение (6) точной производной или нет: 3. Согласно предыдущему предположению,о
для того чтобы формула (6) была точной производной, необходимо и достаточн Людмила Фирмаль
выполнить условие (а). Если выражение (6) является (полной) производной некоторой функции P (x, y), то пусть уравнение (7) имеет место, вам просто нужно обратиться к теореме D R_d2p D0__d2p du DX-9DX du d d X9 (). Перейдем к доказательству D o s t O h n O s t I. Когда выполняется условие (A), мы знаем, что интеграл (3) не зависит от пути интегрирования(теорема 2). В этом случае Интеграл однозначно
определяется назначением точек A(x0, y b) и B (XY z^), которые могут быть обозначены символом по отношению к нему В(!, ^икс) §Р Д х-\ — с^БУ или§р б х-\ — о б. A(x0, Z’o) Сам путь не указан, но он безразличен—можно как-то закрепиться. Если точка A (x0, u0) фиксирована и точка B заменена любой точкой 714 (x, y) в области (B), то Интеграл результата будет разделен на несколько f y n K C от t o h K и 714.): (Х,
- Y) Р(х, г)=я п б х-\ — о Бу. (8) (о; ‘ о) Он показывает, что эта функция является примитивом для выражения (6) и для этой цели имеет дело с проблемой частных производных как в x, так и в Y. Возьмите любую точку в области (x y z^) (7?), дайте приращение XG Ah, точка C(x1 — [- ^x, это 270ch. XXI. двойной Интеграл 1350 Достаточно малый DH будет также принадлежать m E S te (E), включая все o t R E z to o m sun(рис. 36). Соответствующие значения функции (1, С. ) П(ХУ1)=у Rs1h -] — ($s1u, (0. D’O) (l-14-DH), Р(ХГ+Dн, г)=Rlh-\ — S1Yu. (О > З это’о) Для
второго интеграла, который принимает любую кривую (TC), соединяющую первую точку A и B этих интегралов, интегральный путь состоит из той же кривой и прямого отрезка BC. Итак, приращение функции p равно P (1+Y1) — P (1>^1)= =у Р(1Х-]-с}(1У=Р(х, г) ых(против) (против) Поскольку сегмент BC перпендикулярен оси y, интегралы, включая f & y, исчезают. Остаток Интеграла сводится непосредственно к обычному определенному интегралу: для этого в функции парциальной плотности мы заменяем YG на YG (из уравнения y=yg в BC)и обозначаем предел Интеграла x как предел. XI+DH Р(Х1-а — ^х, г К) — Р(х б^1)=(б)р(х, г^г х.
XI Если применить среднюю теорему к обычному полученному интегралу и разделить обе части уравнения Людмила Фирмаль
на DX, то получим、 Давайте теперь направим DH к нулю. Следовательно, в точке (x_) существует частичная производная функции p от x.» ■=р (х»л)§4. Независимое условие криволинейного интеграла 271 Аналогично устанавливается уравнение 34) дю=0. (b UD-так как точка (XY34) была взята произвольно в пределах области (E), то для всех точек в этой области достигается соотношение(7) d P_DX Поскольку эти частные производные непрерывны, функция P (x, y) является производной[n°142]: y P = d^(1x — {- ^a y=P<1x — \ — (^<1U, То, что мы хотели доказать. Такой результат можно вывести из сравнения теорем 1, 2 и 3. В предположении, что для того, чтобы Интеграл (3) не зависел от траектории (а замкнутый Интеграл бы
л равен нулю), необходимо и достаточно, чтобы представление частичной плотности (6) было точной производной. Чтобы доказать теорему 3, мы установили для интеграла кривой(8), а не z b и C I s e g o от пути,переменный верхний предел[n°183,12°]для деления нормального определенного интеграла. Теперь, когда мы знаем примитивную функцию f (x, y) Субинтегрального выражения (6), мы знаем, что наряду с отношением, содержащим функцию (7) (8、 D х~^дю Тогда разность P (x, y) — f (x, y)=C=S81 (ведь частные производные как x, так и y равны нулю!да что с тобой такое? Предполагая X=x0, y=34, Вы получаете C= — f (x0, y0), поэтому, если вы возьмете ( * , Y)=f ( * , Y) — f (o, Y o) — if, и, наконец, здесь x=x и y=y, то вы получите формулу U1 §Р Д х+0^У=Ф(x1u УБ) — Ф(Х О,и U0)=F(х, у)я(9) (АБ)о, у Или, короче
говоря, В Р = ч+<2au=®(в) — Ф(Д)=Ф(М) (9а) (AB) A Эта формула очень похожа на основную формулу для интеграла[n°185] и эквивалентна обычному определенному интегралу в главе 272, XXI. двойной Интеграл[351 Но мы еще раз подчеркиваем, что это относится только к независимым от пути интегралам кривой. Точные характеристики дифференциальных условий(а) восходят к Эйлеру и Клеруту (1740). Кривая интегрирования дифференциального уравнения (6) (без этого Т Е Р М и Н а) также впервые возникает при изучении»л е р о», теории фигуры Земли…»(1743*).) Предполагая, что форма кривой задана как уравнение между x и y, Клеро исключает ее из (6) y и BU и интегрирует полученное уравнение, содержащее только x и DX. Здесь обозначим условие независимости Интеграла кривой крэро:уравнение(6) должно быть совершенным дифференциалом, который должен удовлетворять условию(а).
Смотрите также:
Решение задач по математическому анализу
| Интеграл по простому замкнутому контуру | Приложения к физическим задачам |
| Интеграл по кривой, соединяющей две произвольные точки | Преобразование плоских областей |

