Оглавление:


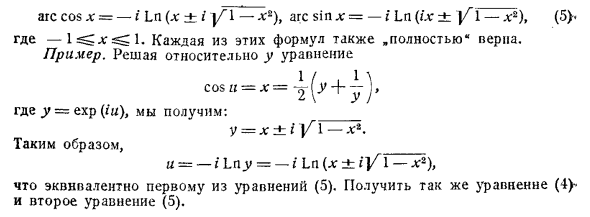
Связь между логарифмической и обратными тригонометрическими функциями
- Связь между логарифмической функцией и обратной тригонометрической функцией. ch, VI, дробно-рациональная или алгебраическая функция a, интеграл от% …, a, (J, … являются константами Часто оно принимает различные формы в зависимости от значения и может быть выражено в логарифме или в обратной тригонометрической функции. Например дх 1. х J ‘ если а> 0, но * -VsL \ (2> DX 1 J в ~ 2 U-a x + U-a Если <0. Эти уравнения показывают, что между логарифмической функцией и обратной тригонометрической функцией должна быть некоторая функциональная связь.
Тот факт, что такая связь действительно существует, можно увидеть из того факта, что тригонометрическая функция C выражается через expiC, а логарифм является функцией обратной экспоненциальной функции, как уже было видно. Давайте рассмотрим отношения J дх 1. X-а Происходит, когда a на самом деле u-> p ^ r положительно. Если вы можете заменить a на a / a в этой формуле, у вас будет следующая формула. Дуга tg- = In + C, <3> 6 a 2l LH -f- ta 1 * Здесь, поскольку C является константой и уже определила логарифм комплексного числа, возникает вопрос, является ли это соотношение истинным. Согласно предыдущему разделу (см. Раздел 231) Ln (xnn b) = 1 Ui (.x2 + a ) ± / (* + 2A-),
Где Λ — целое число, наименьший абсолютный угол, а его длина X даже COS 9 = • -, SIP 9 = -. Yx * + a »yx2 + o * Людмила Фирмаль
| Выражения синуса и косинуса через показательную функцию | Степенной ряд для ехрz |
| Обобщенные гиперболические функции | Логарифмический ряд |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Вот так 1. х-Ia. -rgg- Ln ——r — ‘f-I’, 21 х — я Где / является целым числом, и это последнее выражение действительно отличается » х Из любого значения дуги тг-только постоянные члены. но Основная формула для соединения логарифмической функции и обратной тригонометрической функции заключается в следующем. arc \ gx — u Ln y ^ j ^> (4> х действителен. Это выражение равно nL, а правая часть является выражением 1. cos y -M sin y 1. , , , , __ Ln- 1 .-. ■ = Ln (exp2iy) —y-A-k ~ 2i уютно — я грешу 2/4 года «* » Где k — произвольное целое число Таким образом, уравнение (4) является «полностью» верным (см. Пример XCIV.3).
дуга cos x = -i Ln {x ± i 1-l; 2), arc sin l; = -i Ln (ix ±] f 1-x2), (5) Где -я ^ я ^ я Каждое из этих выражений также совершенно правильно. 1 /, 1 \ cos u-x = * 2 Где y = exp (iu), где: y = x ± i V1 — V2. Так _ И -i Lny = -i Ln (x ± iV 1-Xs), Это эквивалентно первому в уравнении (5). Получите то же выражение (4) и второе выражение (5).
Читатель также может проверить формулу. Людмила Фирмаль

