Оглавление:
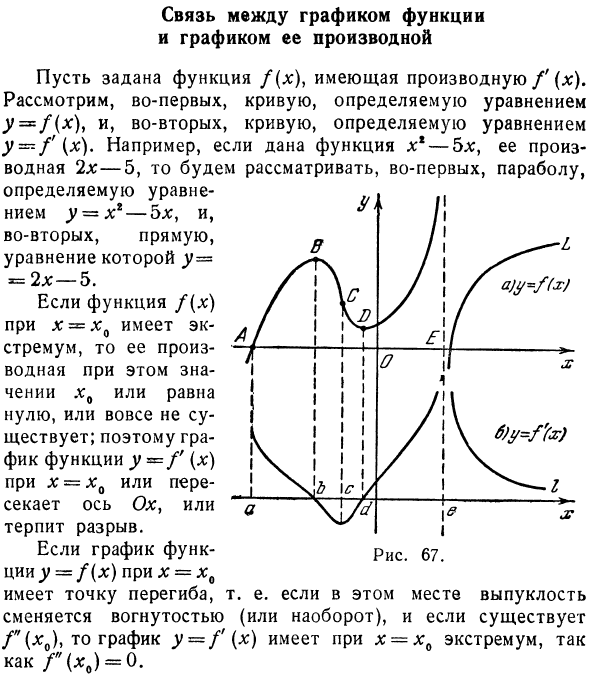



Связь между графиком функции и графиком ее производной
- Связь между графом функции и ее производным графом Дает функцию f (x;) с производной f (x). Сначала рассмотрим кривую, определяемую уравнением y = f (* ), а затем рассмотрим кривую, определенную уравнениями y — f (). Например, учитывая функцию xx-5l, ее производная равна 2x-5, сначала рассмотрим параболу, определяемую уравнениями y-x2-5a, а затем рассмотрим уравнение y = 2x line симы 5. Если функция f (x) для x = x0 имеет экстремальное значение, производная от этого значения .v0 равна нулю или отсутствует вообще.
Когда график функционирует Если x = x0, y = f (x) Есть точка перегиба. То есть, если выпуклая поверхность заменяется вогнутой поверхностью в этой точке (или наоборот), если f «(x0) существует, граф y = f ‘(x) имеет экстремальное значение x = x0 и f (*) .) = 0. Кроме того, в этом разделе все обсуждения и выводы основаны на графиках, поэтому абсолютная точность не требуется.
Поэтому график функции y — f (x 🙂 при x = x0 пересекает или ломает ось Ox. Людмила Фирмаль
Это означает, что здесь проводится только качественное исследование. Поэтому функция f (x) определяется графиком, показанным на рисунке. 67, а. Ниже графика функции y ~ / (x) создайте график функции y-f ‘(x). На обеих фигурах (a и b) точка с одной и той же абсциссой находится на одной прямой, параллельной оси Oy. В отрезке AB функция f (x) увеличивается, поэтому ее производная положительна, но эта функция Если сечение выпуклое, производная уменьшается.
Поэтому график функции y = f (x) в соответствующем разделе ab определяет положительную убывающую кривую. Максимальное значение 67,6 функции f (x) (точка B) на рисунке соответствует пересечению Ось и ось (точка б). Кривая уменьшается в разрезе ВС (рис. 67, а). Поэтому соответствующий участок кривой y = • / ‘(L;) находится ниже оси Ox и уменьшается. Точка перегиба на рисунке 67, соответствующая минимуму на рисунке 67.6. По крайней мере, на рисунке. На фиг.67 (точка D) соответствует пересечению с осью Ox (точка d).
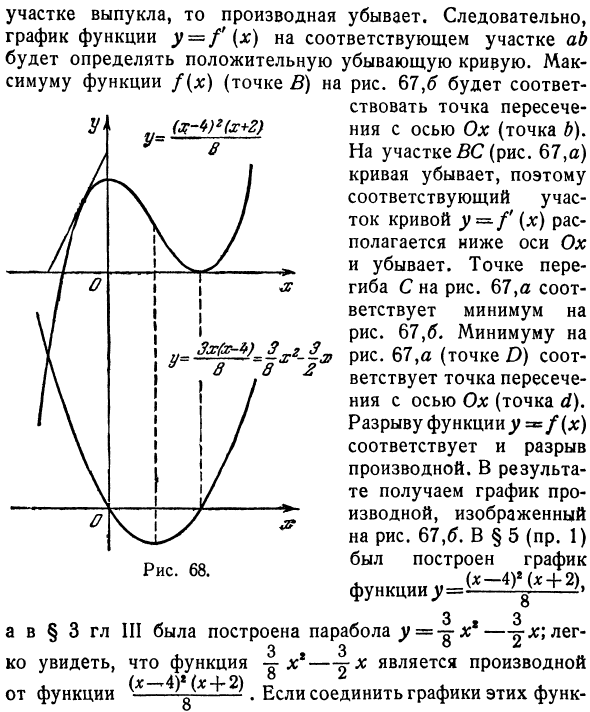
- Разрыв функции y = f (x) также соответствует разрыву производной. В результате получается дифференциальный график, показанный на рисунке. 67,6. График был создан в §5 (пр.1) _ (* -4) ”(* + 2), 8 3 3 А в § 3 главы 3 была построена парабола y = -tr xr-tr ;; 3 3 Убедитесь, что функция x * — ^ x является производной от функции +. Соединяя графики этих функций, (* — *) ‘(X + 2) Рисунок 68.
Функция ^И тогда мы получаем рис. 68. Эта цифра подтверждает вышесказанное. Людмила Фирмаль
Смотрите также:
| Выпуклость и вогнутость линии. Точка перегиба | Бесконечно малые величины |
| Общий план исследования функций и построения графиков | Дифференциал |

