Оглавление:








Свойства коэффициентов множественной регрессии
- Свойства коэффициента множественной регрессии Как и регрессионный анализ, коэффициент регрессии Следующее должно рассматриваться как особый вид случайной величины: Потому что ингредиенты чая присутствуют в случайной модели Для. Каждый коэффициент регрессии у и Независимая переменная в образце и y определяются независимо Переменная Сима и случайный член.
- В результате коэффициент Коэффициент регрессии фактически определяется независимыми переходными значениями. Переменные и случайные члены, а также их свойства сильно зависят от свойств Последний. Условие Гаусса-Маркова выполнено и имя Однако 1) математическое ожидание равно нулю для любого наблюдения. 2) Теорема Статистическая дисперсия распределения одинакова для всех наблюдений.
3) их Орутическая ковариация этого значения для любых двух наблюдений равна нулю. Людмила Фирмаль
4) Независимо от распространения и объяснения перевода перевода Может быть изменено. Первые три условия совпадают с условиями парной регрессии Четвертое условие — обобщение аналога. здесь Настал момент принятия расширенной версии четвертого условия, при условии, что не выполнены следующие условия: Зависимая переменная не является стохастической. Это процент рабочей силы в Соединенных Штатах. (Ред.)
Есть еще два практических требования. Сначала вы должны иметь до Достаточно данных, чтобы нарисовать линию регрессии, Наличие такого количества (независимых) наблюдений, как количество обязательных параметров Я могу поблагодарить вас. Затем, как описано далее в этом разделе, Переменные не должны иметь строгие линейные отношения.
Объективно В двух случаях bx указывает на несмещенную оценку p. Пояснительная переменная. Доказательство легко обобщить Алгебра обучающей матрицы любого числа объясняющих переменных. Как видно Из уравнения (5.12) величина bx является функцией от x p x2 и y. у определяется х2 и и. В результате сумма b {на самом деле зависит хит со значением х p x2 и sample (понимают природу преобразования и могут быть опущены)
Чтобы добавить детали математического расчета): = Cov (X), y) Vag (x2) -Cov (x2, y) Cov (x}, x2) = Var (x!) Var (x2) — {Cov ^, x2)} 2 = — {Cov (xb {a + Pi * i + P2 * 2 + w}) Var (x2) — -Cov (x2, {a + PJX! + P2x2 + и} USow (xxx2)} = = l {[PIVar (x1) + p2Cov (xI, x2) + Cov (x1, «)] Var (x2) — D 4PiCov (xbx2) + P2Var (x2) + Cov (x2iu)] Cov (xbx2)} = = l {P1A + Cov (x1, w) Var (x2) -Cov (x2, w) Cov (x1, x2)} = = p1 + i {Cov (x1, t /) Var (x2) -Cov (x2, «) Cov (x1, x2)}, (5.33) Где A есть Var (x {) Var (x2) — {Cov (xp x2)} 2.
Следовательно, величина b {два ω Настройки: истинное значение p и ошибка компонента. Перейти к друзьям Ожидание мы получаем: Эй) = P! + I {Var (x2) £ [Cov (x1, ii)] -Cov (x1, x2) £ [Cov (x2, w)]} = plf (5.34) При условии, что четвертое условие Гаусса-Маркова выполнено. Точность коэффициента множественной регрессии В теореме Гаусса — Маркова для множественного регрессионного анализа.
Для парной регрессии, обычный метод наименьших квадратов Крыса (OLS) обеспечивает наиболее эффективную линейную оценку в следующем смысле: Не могу найти другую информацию, не являющуюся образцом, основанную на той же информации о образце 147 Состояние Ха Усса Марков. Эта теорема не доказывает, но мы изучаем факторы Отрегулируйте возможную точность коэффициентов регрессии.
В общем Кроме того, коэффициенты регрессии наиболее вероятны Точность: 1) Чем больше наблюдений имеет образец. 2) дисперсия пояснительной переменной выборки велика. 3) Теоретическая дисперсия случайных членов мала. 4) Несвязанные вещи являются объясняющими переменными.
Первые три из желаемых условий повторяются, что уже остановлено Для парного регрессионного анализа. Только 4-е условие Новый. Сначала давайте посмотрим на случай, когда есть два независимых изменения Затем перейдем к более общему случаю. 2 независимых переменных Если истинные отношения: y = a + p ^ j + p2x2 + u, (5.35) И вы получили уравнение регрессии y = a + ft, * i + bjc2, (5.36)
Теоретическое распределение вероятностей с использованием необходимых данных Распределение bx описывается следующей формулой: Где GU2 — теоретическая дисперсия и. Аналогичная формула Замените Var (x {) на Var (JC2), чтобы получить значение b2 теоретической дисперсии. Из уравнения (5.37), как и в случае парной регрессии.
При анализе желательно, чтобы количество n и Var (x () было большим, маскировать и 2- маленький Тем не менее, теперь (1-г ^ XI) е и Не ясно, что слабая корреляция между x1 и x2 желательна. Интуитивное объяснение легко. Правда если Формат зависимости выглядит следующим образом: у = 2 + 3х, + х2 + и. (5,38) Предположим, что существует неточная линейная зависимость между xx и x2 Мост: * 2 = 2x, -1 (5,39)
И предположим, что хх увеличивается на одну единицу. Все наблюдатели Дения. Затем x2 увеличивается на 2 единицы, а y-5 единиц. Но например на столе. 5.2 При просмотре этих данных вы можете получить доступ к одному из следующих: Акватория: 1) Количество у определяется по формуле (5.38) (правильное описание п);
2) Значение х2 не имеет значения в этом случае значение у Определяется зависимостями. у = 1 + 5 * j + и; 3) Количество х {в этом случае количество у оп Поделиться с: у = 3,5 + 2,5х2 + и. На самом деле бизнес не ограничивается этими возможностями. любой Зависимость (средневзвешенное по условиям (2) и (3)) Соответствует описанным данным.
Условие (1) можно представить следующим образом Условно-взвешенный средний (2) коэффициент равен 0,6, (3) коэффициент равен Том 0.4. Когда использовать регрессионный анализ или другие методы В этом случае трудно различить эти возможности. Значение и оценочное значение результата будут очень чувствительными Случайные участники.
Может содержать серьезные ошибки. Коэффициент дисперсии Коэффициент регрессии велик, но это явно другой путь Бум того же выражения. Когда истинная зависимость (5.39) является строгой, при оценке Становится невозможным различить все вероятности Зависимости. Потому что каждый соответствует одинаково хорошо Запрос данных.
Вы даже не можете рассчитать коэффициенты регрессии. Это связано с тем, что числитель и знаменатель уравнения (5.12) равны нулю. Коэффициент, если между Xj и x2 существует неточная линейная зависимость Коэффициент корреляции rXXiX2 близок к 1, когда зависимость.
Если зависимость отрицательная, это целое число минус 1, и в обоих случаях привет гх х ^ близко к 1. В результате знаменатель второго члена уравнения Согласно (5.37), оно близко к нулю, теоретическая дисперсия b {и b Большие цифры. Ограниченный случай существования точной линейной зависимости Распределенные мосты имеют тенденцию быть бесконечными.
- Обратите внимание, что количества bx и br не отслеживаются автоматически. Если есть большая теоретическая разница и между ними не точно между х Линейные отношения. Дисперсия также зависит от l и aw2 как в паре Регрессионный анализ. Если n велико, а a2 мало, теоретическое Несмотря на слабую линейную зависимость, персидские bx и b2 могут быть небольшими Значение.
Когда информации много (n большое) и случайных фактов Тор относительно не важен (а2 маленький) Рассмотрим влияние х и х2 на значение у. Общий случай Не выводите уравнение для дисперсии коэффициента регрессии Общий случай.
Как и формула самих коэффициентов, они лучшие Рассчитать, используя матричную алгебру. Людмила Фирмаль
Вместо этого отображается один важный момент, основанный на эксперименте. По методу Монте-Карло. Согласно условию (4) Мои переменные не были тесно связаны. Оцените, чтобы исследовать это 3 регрессии. Во-первых, независимая переменная Если это слишком тесно связано, результаты регрессионной оценки являются надежными Во-вторых, тесная связь между переменными приводит к Регрессия содержит ошибки.
И в-третьих, с таким же близким COR Связь между независимыми переменными, но меньше дисперсии Результаты регрессионной оценки членов чая были значительно улучшены. Это показывает тесную корреляцию между независимыми переменными Это может привести к неудовлетворительным результатам, но этого не происходит Помидор.
Это также зависит от дисперсии случайного члена. Предположим, что заработная плата в стране >> определяется числом Записки лет обучения (5), истории работы (X), возраста (A) и случая. Bas Зарплата составляет 10000 и 1500 добавляется к каждому. 500 лет работы каждый год, минимум 10 лет исследований 25-Каждый год ты жил.
Кроме того, есть случайные факторы, которые: у = 10000 + 1500 (5-10) + 500 * + 25A + и (5.40) В результате упрощения это уравнение выполняется в следующем виде: y = -5000 + \ 500S + 500 * + 25A + и (5,41) Первые 4 столбца таблицы. 5.3 Представляет воображаемые данные выбора Ки из 20. Период исследования, история работы и возрастные ценности Это было принято произвольно.
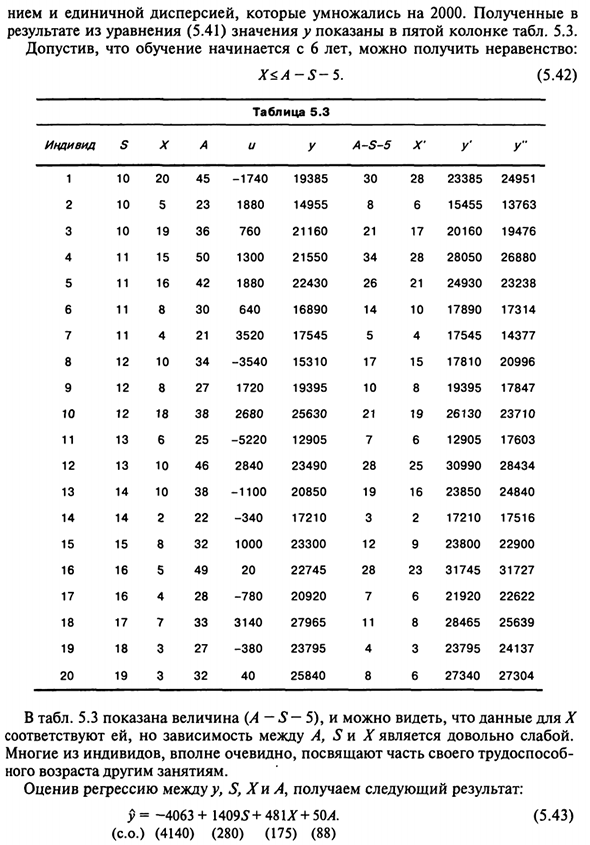
И значение было определено на основе образца из 20 лунок Случайно распределенные случайные числа с нулевым математическим ожиданием 150 Единственная дисперсия, умноженная на 2000. В результате по формуле (5.41) значение y отображается в пятом столбце таблицы. 5.3. Предполагая, что обучение начинается в 6 лет, вы можете получить неравенство. X <A-S-5. (5,42)
В таблице. 5.3 отображается значение (A-S-5), и вы видите, что отображаются данные X. Хотя они согласны, отношения между A, S и X довольно слабые. Многие люди явно преданы некоторым своим рабочим возможностям. Возраст для других видов деятельности. Оценка регрессии между y, S и ChiA дает следующий результат: y = -4063 + 14095+ 481LG + 50A (5,43) (Совместный) (4140) (280) (175) (88) 151
Эксперимент был повторен с использованием тех же данных и одинаковых значений для S и A. С другим набором данных Ями, но Ху намного лучше В сочетании с индикатором {A-5-5). Эти данные приведены в таблице. 5.3 Метод X \ re Результирующее значение y отображается как y . В любом случае оно становится почти равным и затем может наблюдаться нестабильно.
Линейная связь между независимыми переменными. Рег рейтинг \ Сечение между S и X’iA выглядит следующим образом. >> = -7524 + 7815-207LG + 664L. (Co.) (4204) (529) (538) (476) (5,44) В настоящее время результаты регрессионной оценки очень плохие. Наконец, эксперимент был повторен при сохранении того же S, A, X значения \ однако, получить значение и умножить его случайным образом Число 200 вместо 2000.
Значение результата у показано в таблице. 5.3 Метод Оценка регрессии между y \ y «, S, X и A дает у = -5252 + 14285 + 429Х + 89А. (5,45) (Ко.) (420) (53) (54) (48) За исключением фактора А, эти результаты очень удовлетворительные. Смертельно, несмотря на существование неточной линейной зависимости Между независимыми переменными.
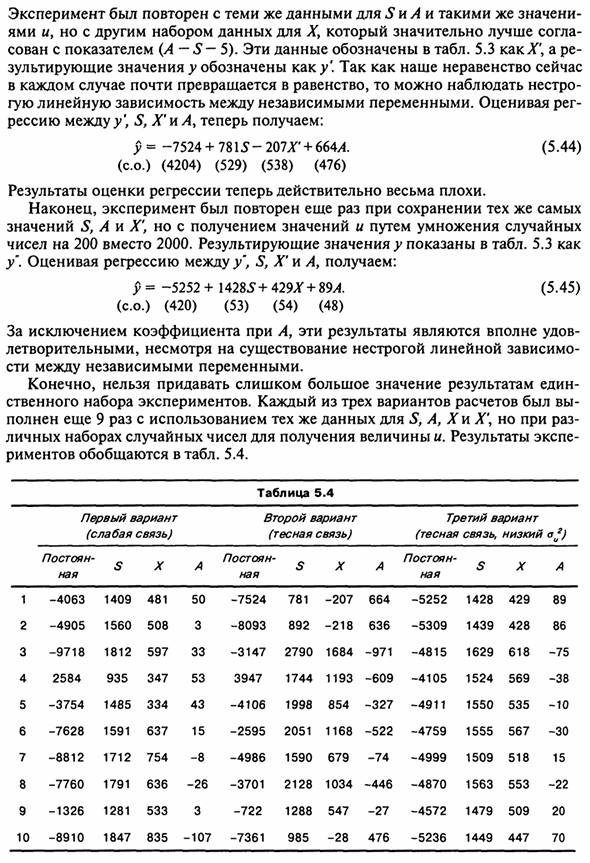
Конечно, вы не можете сосредоточиться на одном результате Естественный набор экспериментов. Каждый из трех вариантов расчета был вами Завершите еще 9 раз, используя те же данные для S, A, X и X, но иногда Персональный набор случайных чисел для получения величины. EXP результаты Исследования сведены в таблицу. 5.4. 1 2 3 4 5 6 7 8 9 10
Первый вариант (Слабая связь) постоянная не -4063 -4905 -9718 2584 -3754 -7628 -8812 -7760 -1326 -8910 S 1409 1560 1812 +935 1485 1591 1712 1791 1281 1847 X 481 508 597 347 334 637 754 636 533 835 50 3 33 53 43 15 -8 -26 3 -107 Таблица 5.4 Второй вариант (Близкие отношения) постоянная не -7524 -8093 -3147 3947 -4106 -2595 -4986 -3701 -722 -7361 S +781 892 2790 1744 1998 2051 1590 2128 1288 +985 X -207 -218 1684 1193 +854 1168 +679 1034 547 -28 664 636 -971 -609 -327 -522 -74 -446 -27 476
Третий вариант (Закрыть постоянная не -5252 -5309 -4815 -4105 -4911 -4759 -4999 -4870 -4572 -5236 связь S 1428 1439 1629 1524 1550 1555 1509 1563 1479 1449 низкий) X 429 428 618 569 535 567 518 553 509 447 89 86 -75 -38 -10 -30 15 -22 20 70 152 При просмотре таблицы. 5.4 Сосредоточиться на соотношении В S и X. Коэффициенты и константы в A case: коэффициент A имеет истинное значение, близкое к нулю.
Точки, определяемые условиями: 5 * = 0, ^ = 0, Λ = 0, Довольно далеко от диапазона выборки. В первом варианте осуществления коэффициенты S и X обычно желательны. Диапазон. Во второй версии они безнадежно неточны, а в третьей — все они Ма это хорошо. Результаты эксперимента сведены в таблицу. 5.5. Обратите внимание, что нет смещения, характеризуемого тенденциями.
Его коэффициенты систематически выше или ниже, чем их истинные Значение также во второй версии, результат очень неточный. второй Средние значения коэффициентов для варианта S и ^ равны Будь то 1624 и 671. Это не так далеко от истинного значения. Стандартная ошибка коэффициента регрессии Стандартные ошибки множественных коэффициентов регрессии включают.
То же самое, что и анализ парной регрессии Оценивается по стандартному отклонению распределения коэффициентов регрессии Они связаны с их истинным значением (см. Раздел 3.5). Как парная регрессия В анализе стандартное уравнение ошибки Распределение и уравнение с заменой st2 несмещенными оценками Извлечение квадратного корня.
Как и прежде, важность полученной формулы Следовательно, это правильная спецификация модели и Условие Гаусса – случайного слагаемого Маркова. рассеивание Случайный участник низкий высокая Таблица 5.5 Линейные отношения между Независимая переменная слабый отравление.
Будьте надежны приемлемый близко отравление приемлемый Это нельзя доверять Например, если есть только две независимые переменные, Визуальная дисперсия коэффициента регрессии b (выражается уравнением (5.37)). В этом случае несмещенная оценка a2 равна Получается умножением величины Var (e). Боковая дисперсия остатков, п / (п-3). так соГМ-J «х] — ((* /» — 3) Вай (э), сГ wVarCxj) l-r2 J nUat (x {) l-r2 X \ UX2 I x \ ix2 Вар (г) 1 / I-3Var (x)) Xi_r2x, x • 2 (5,46)
Соответствующую формулу для стандартной ошибки b2 можно получить по следующей формуле. Индекс перестановки темы. Если существует более двух независимых переменных, гораздо удобнее выразить От стандартной ошибки и самого коэффициента регрессии Степень матричной алгебры. В начале этого раздела были разработаны четыре условия.
Это дает надежную оценку коэффициента рег. рессия, прямое расследование третьего и четвертого условий На основе экспериментов Монте-Карло. Каждое условие отражается в Уравнение для дисперсии коэффициента регрессии показано в уравнении (5.37), и каждый из них отражается в соотношении (5.46).
В частности, тесная линейная связь между двумя объяснительными изменениями Значение приводит к получению значения г ^ близко к 1. Конечно, стандартная ошибка (setrispalybus) является относительной Однако, поскольку он велик и отражает неточность коэффициента регрессии, То, что мы видели раньше. Например, стандарт Ошибка в уравнении (5.44).
Наблюдалась тесная линейная связь между S и X. А, намного больше, чем стандартная ошибка уравнения (5.43), это соотношение Это было слабым. Кроме того, рекомендуется сравнить стандартную ошибку уравнений (5.44) И (5.45). В начале их значения были получены путем умножения случайным образом Цифры до 2000 года. Во втором числе мы умножили эти числа на 200.
В результате оценки, Регрессия уравнения (5.45) была гораздо более точной. Гораздо меньшая ошибка. Коэффициент регрессии составил 10 раз Она (если учитывать разницу между оценкой и истинным значением) и Стандартная ошибка была только 1 / оригинальный размер. t-критерий и доверительный интервал Испытание коэффициента множественной регрессии f выполняется таким же образом Как сделано в парном регрессионном анализе.
Обратите внимание, что важно Уровень / уровень важности зависит от количества степеней свободы, (N-k-1): количество наблюдаемых значений минус количество оцененных параметров Groove (один коэффициент для каждой независимой переменной и константы Пользователи).
Доверительные интервалы определяются точно так же, как спаривание Регрессионный анализ, в соответствии с указанными примечаниями Степени свободы. упражнения 5,7. Линейная регрессия и логарифмическая регрессия (5,2 и 5,5 движений) Личные доходы и расходы на жилье По цене этих услуг это выглядит так (стандартная ошибка показана в скобках):
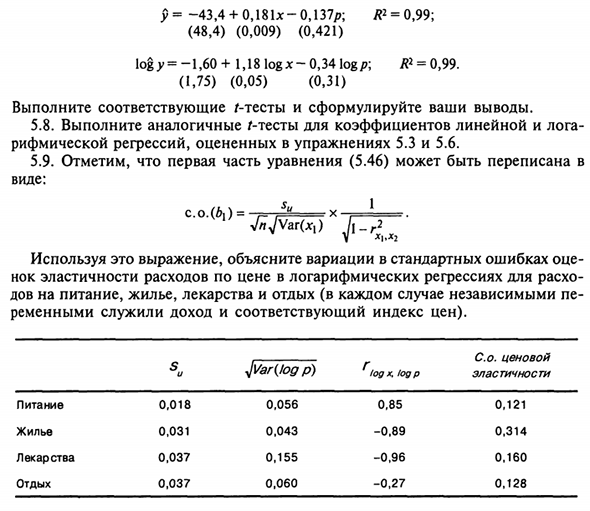
154 р = -43,4 + 0,181х-0,137р; / р = 0,99; (48,4) (0,009) (0,421) log ^ = -1,60 + 1,18 log * -0,34 logp; R2 = 0,99. (1,75) (0,05) (0,31) Запустите соответствующие / тесты и сделайте выводы. 5,8. Провести аналогичные / -тесты по линейным и логарифмическим коэффициентам Регрессия рифмы оценивается в упражнениях 5.3 и 5.6. 5.9.
Первая часть уравнения (5.46) Форма: сотрудничество. (Z>,) = * «1 Используйте это уравнение для описания стандартного изменения ошибки Ценовая эластичность затрат на потребление логарифмическая регрессия Еда, жилье, лекарства, отдых (каждый независимый Выручка и соответствующие ценовые метрики служили переменными). питание корпус медицина перерыв S и 0,01 8 0031 0037 0037 ^ WagCode p) 0,056 0043 0,155 0060 Туман x, log p 0,85 -0,89 -0,96 -0,27 A. цена эластичность 0,121 0,31 4 0,160 0,128
Смотрите также:
| Множественная регрессия в нелинейных моделях | Мультиколлинеарность |
| Что можно сделать в случае гетероскедастичности? | Качество оценивания: коэффициент R2 |
Если вам потребуется заказать решение эконометрики вы всегда можете написать мне в whatsapp.

