Оглавление:

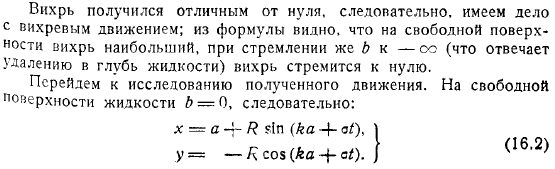




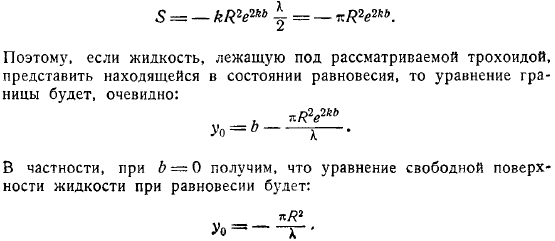



Свойства трохоидальных волн
Это указывает на то, что полученное движение является. To сделайте это, вычислите скорость вихря. Для компонентов скорости. Для этого в правой части уравнения. Решите эти уравнения относительно: Найти таким же образом. Следовательно. Поскольку вихрь оказался ненулевым, мы имеем дело с вихревым движением.
Из уравнения видно, что вихри являются наибольшими на свободной поверхности, в то время как вихри стремятся к нулю (соответствуют удалению в жидкую среду). Перейдем к изучению полученного движения. Поэтому на свободной поверхности жидкости. Такие частицы исследуются в.
- Получается, что каждая частица рисует круг с радиусом. Кроме того, период вращения и скорость частиц равны. Если угловая разность равна, то частицы с разными частицами будут находиться в одной фазе.
- Эти частицы разделены некоторым расстоянием. Это явно длина волны.
Профиль волны (пунктирная кривая) в определенный момент времени выражается в виде параметра уравнением и параметром является. Людмила Фирмаль
Примите, чтобы быть легким. Затем введя угол, мы получаем гидромеханику. Как известно, в этом и заключается суть трохоида.
Другими словами, это кривая, нарисованная точкой в катящемся круге на прямой. Фактически, рассмотрим прокатку радиусного круга без скольжения по прямой, параллельной оси и отстоящей от оси вверх. Если круг поворачивается на угол волны Герстнера. Центр круга отходит
- Поэтому координаты точки, в которой точка продвигается, очевидно, справедливы.
- Если трохоид берется без петля, циклоида соединена (она есть точка возврата первого рода). Наконец, используйте трохоид с петлей. Последний случай явно физический.
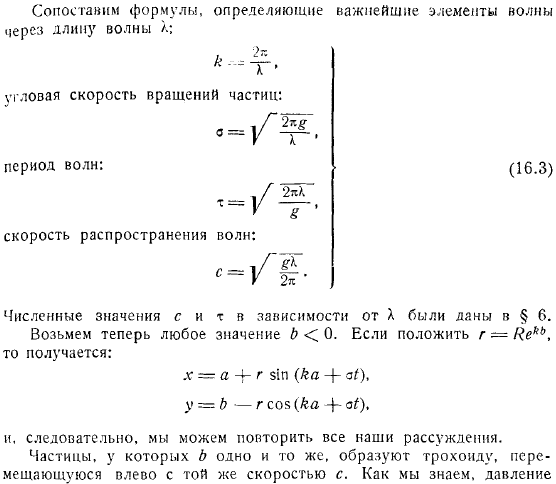
Мы должны считать. Очевидно, что профиль волны движется влево вместе с. Также показано, как получить очевидный профиль волны из чертежа. Сравните уравнения, которые определяют наиболее важные элементы волн через длину волны энергии волн. Скорость вращения частиц: период волны. Скорость распространения волн: Приводились цифры и зависимости.
Теперь давайте возьмем любое значение. Людмила Фирмаль
Если поставить, то получается. Поэтому можно повторить все рассуждения. Частицы с теми же самыми образуют трохоид, который движется влево с тем же самым. Вы знаете, давление то же самое во всех точках этого трохоида, а именно.
С тех пор радиус круга, описываемого частицами, будет меньше, а рассматриваемые частицы будут глубже. Отображается общий вид движения. Он представляет собой трохоид, соответствующий эквидистантному значению (все эти трохоиды служат свободными поверхностями жидкостей, так как они являются горизонтальными плоскостями, то есть поверхностями с одинаковым давлением).
Таким образом, радиус окружности уменьшается экспоненциально. Наконец, пунктирная линия представляет собой линию, в которой находятся частицы с одинаковыми координатами. Рассмотрим вопрос о том, как жидкость находится в равновесии, то есть каковы будут координаты частиц с Лагранжевыми координатами.
Напишите уравнение трохоида, которое соответствует постоянному значению параметра. Представляет собой область, окруженную трохоидом и линией (часть области выше этой линии считается положительной, а ниже-отрицательной). С тех пор Очевидно.
Это значит итак, если жидкость под рассматриваемым трохоидом представлена в равновесном состоянии, то граничное уравнение становится понятным. В частности, уравнение свободной поверхности жидкости, находящейся в состоянии равновесия, выглядит так. Именно поэтому гребень волны находится выше поверхности нежной жидкости, а размер подошвы-ниже поверхности.
Путем успокаивать жидкость. Что касается отношения между, по сути, рассматривая элементы плоскости в плоскости, площадь в плоскости равна. И площадь положения равновесия жидкости. Эти площади должны быть равны. Кроме того, площадь, ограниченная вертикальными линиями на расстоянии, равном соседним трохоидам, равна.
Очевидно, что высота рассматриваемой волны одинакова. Так как эта высота никогда не может быть превышена Также отметим, что предельным профилем волны в нашей стране является циклоида с острием первого рода. Теория показывает, что волны без вихрей имеют различные типы предельных профилей. Высота этой предельной волны значительно меньше, чем в случае трохоидной волны, и не достигает четных чисел.

