Оглавление:







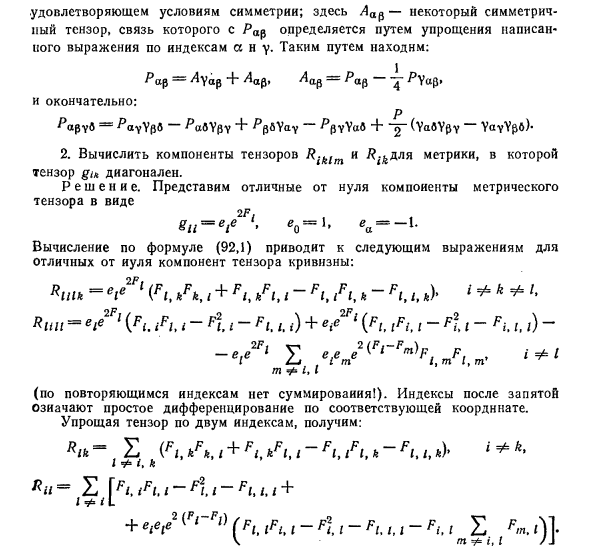

Свойства тензора кривизны
- Свойство тензора кривизны. Тензоры кривизны имеют гендерную симметрию Определите, что нужно получить из смешанных компонентов Nent R lkim ковариат: Риклм-СинР клм • Вы можете легко получить о них с помощью простого преобразования. Формула: О _ 1 (d2gim. D2gki d2gu d2gkm \ ■ W N W 2 ^ d x kd x l -h d x id x m d x kd x m d x id x l) + gnP (r2, rL-rL. rS). (92-1)
Из этого уравнения очевидны следующие свойства симметрии: рИИ: Riklm = Rkilm = Rikmh (92,2) Риклм = Римик) (92,3) То есть тензор асимметричен в каждой паре индексов ik и lm И симметрично относительно перестановки каждой из этих двух пар Свойства тензора кривизны 353 С друзьями
что циклическая сумма равна нулю Из компонента Рикирм Людмила Фирмаль
В частности, все компоненты Rikirm являются диагональными Индексная пара gk или 1t равна нулю. Кроме того, легко убедиться, , образованного любыми тремя индексами Сова, например: Rikim «b Rimkl» b Rilmk = 0 (92,4) (Другие отношения такого рода взяты из (92.4) Математически по свойствам (92.2), (92.3)). Наконец, докажите следующую личность Бьянки: R nikl; m + R nimk; l + R ^ г / га; / s = 0. (92,5)
- Полезно проверить, используя локальную геодезическую линию Система координат. Каждый для тензорных символов Таким образом, решение (92.5) справедливо во всех других областях. Система. Дифференциация и настройка уравнения (91.4) Есть Thk1 = 0 и найти точку проблемы т = дРники д2т д2т? К ихм дхт дхтдхк дхтд1- Используя эту формулу, (92.5) Это действительно происходит. Может быть построен из тензора кривизны путем упрощения Тензор второго ранга.
Это упрощение может быть сделано только. Один из методов: упрощение тензора Рикима с индексами g и k или / И w будет равно нулю благодаря их антисимметрии. Для других пар, до знака Результат. Определить тензор R ^ (это называется тензор Богатый) Rik = g lmRlimk = R lilk • (92,6) Согласно (91.4) e> __ ZTts! -r / -ult fa n ~~ dhG ~~ dhk iklrn ~ il krn ‘Vy2 * 7J
Это называется скалярной кривизной пространства Людмила Фирмаль
Этот тензор явно симметричен: Рик = Рки- (92,8) Наконец, упростим R ^, чтобы получить инварианты R = gikR ik = gilgkm Риким, (92,9) . Тензорный компонент дифференциально выполняется Идентичность, полученная путем упрощения личности Биана Индекс ik и пара ki (92,5): (9 2 ‘1 0) (92.2) — (92.4), не все компоненты тензора, в зависимости от соотношения Кривизна не зависит.
Определить количество независимых компонентов Компонент. Определение заданного тензора кривизны Относится к любому количеству пробелов по формуле Колено Сначала рассмотрим случай двумерного пространства. Т.е. нормальная поверхность, в данном случае показана Тензор кривизны с точки зрения Pabc <di) Метрический тензор через 7a &, где индекс a, b, … Значения 1 и 2.
Каждая пара ab и cd имеет два индекса Если это должно иметь другое значение, ясно, что все по-другому Совпадение ненулевой компоненты тензора кривизны Мой друг или знак отличается. В этом случае Например, существует только один независимый компонент, такой как Pi2i2-. Легко видеть, что скалярная кривизна в этом случае равна p _ 2 P1212 ^ ^ ^ | | | | _ ^ и ^ 22 _ (92.11) 7
Значение P / 2 соответствует так называемой гауссовой кривизне Поверхность К: Ј = # = -, (92.12) Где p i и p2 — основные радиусы кривизны для данной поверхности. Напомним, что точки (p1 и p2 считаются одинаковыми Символ, когда расположен соответствующий центр кривизны
Если на одной стороне поверхности есть другой знак, Центр кривизны находится на противоположной стороне поверхности. в K> 0 в первом случае, K <0) x во втором случае). Перейдите к тензору кривизны в трехмерном пространстве. Он выражается как Pa ^ s ^, а метрический тензор — как 7a / #. Здесь, Индекс а, / 3, … выполнить значения 1, 2, 3
Индексная пара af3 и 7 # запускаются только 3 разных сета Значения: 23, 31, 12 (изменить только перестановку парных индексов Знак тензорной составляющей). Поскольку тензор Pa / 3 ^ 6 симметричен Существует только 3 * 2/2 = для перестановок этих пар. = 3 независимых компонента с разными индексными парами и Также три компонента с одинаковой парой.
Идентичность (92,4) Новые не будут добавлены к этим ограничениям. так В 3D тензор кривизны равен 6 Независимый компонент. Такое же количество компонентов обладает симметрией. Тензор Ra / S Поэтому линейные отношения Пап = -P ^ a§ / может представлять все компоненты трех тензоров Pa ^ s Через Пап и метрический тензор 7ап (см. Выпуск 1).
Если вы выбираете Система координат, декартовы координаты в данной точке, затем соответствующие Поверните его, чтобы переместить тензор круга к шпинделю 1). Следовательно, кривизна каждого трехмерного пространства Точки определяются тремя величинами 2). Наконец, перейдите к 4D пространству. пара Индекс ik l 1t работает в этом случае 6 различных наборов Значение канавки: 01, 02, 03, 23, 31, 12.
Таким образом, есть шесть компонентов. Риким Нент одинаков, 6 * 5/2 = 15 разных компонентов Индексная пара. Тем не менее, последние еще не все независимы Отдельно: 3 компонента со всеми 4 индексами Подключайтесь по-другому, благодаря одному ID (92.4): Рон + доза 12 + D0231 = 0. (92.13) Таким образом, в 4 пространствах тензор кривизны 20 независимых компонентов.
Система координат, Галилея в указанной точке, и Посмотрите на преобразование, которое вращает эту систему значение г ^ не изменяется в определенной точке), может быть достигнуто Исчезновение шести компонент тензора кривизны (6 — число независимых поворотов четырех координатной системы).
так Поэтому в общем случае кривизна четырех пространств определяется. 14 величин в каждой точке. При Rik = О1) тензор находится в произвольной системе координат. В кривизне всего 10 независимых компонентов. соответствующий Преобразование координат, тогда тензор Риклма можно уменьшить В «стандартном» формате (в определенной точке 4 пробела)
Его компонент представлен 4 в общем случае. Независимое значение, в особых случаях это число может подойти Сделайте это еще меньше. То же относится и к Rikφ0 Тензор кривизны после разделения определенных частей, Представлено компонентом R ^. Т.е. настроить 10 zor2) Ciklm = Riklm 2 ^ ilgkm 2 ^ im8 kl ~ \ ~ «B ~ Rklgim ~~ RkmgilН» ~ R {gilgkm ~ gimgkl) • (92.14)
Вы можете легко увидеть, что этот тензор обладает всеми свойствами сима Тензорная метрика Риклма? При складывании указателей пар (ил Или ct) дать ноль. Указывает, как классификация построена. Каноническая форма тензора кривизны при = 0 (А. 3. Петров, 1950). 4 Взвешивание в данной точке пространства Уменьшено до Галилея.
20 независимых коллекций Тензор ингредиента Риклм представлен в виде комбинации трех Размерный тензор, определяемый как: Aa (3 = R0ct0 / 3j Ca / 3 = «ea7 <5e / 3A / l- ^ 7 <5A / L7 = до ea ^ 6- ^ 013 ^ 6 (92.15) (Ea /? 7 — единичный антисимметричный тензор. Трехмерная метрика является декартовой и не должна быть связана с суммой. Глобальное различие между верхним и нижним индексами).
Тензоры Aar и Sar по определению симметричны. Тензорные переменные, Вообще говоря, он асимметричен и его след равен нулю в s Лу (92,13). Согласно определению (92.15), например: B c = я? 0123> B 21 = D13BI- ^ 0112, C c = i? 2323, ••• Легко видеть, что условия эквивалентны Rkm-8 g1 Likim-0.
Эти отношения между компонентами тензора (92.15): Ааа-0? Var = Vra, Aa (3 = ~ Ca @. (92.16) Далее я введу симметричный комплексный тензор. Да / 3 = ^ (Аа / с + 2 гВА / с-Са / с) = Аар + иБа / 3. (92.17) Комбинируя два настоящих 3D тензора Аар вот так Если Var — комплексный тензор, он соответствует объединению. Связь двух векторов E и H с комплексным вектором F (глава 25) и Связь между Dap и 4-тензорным Rikim Соответствует связи между F и 4 тензором F ^.
Продолжение следует 4D-преобразование тензора Рикима эквивалентно 3D сложное вращение, генерируемое на тензоре Лямбдаф 3. Могут быть определены в отношении этих изгибов Собственное значение A = Xf + i \ ff и собственный вектор pa (Вообще говоря, сложный) Как решение для одновременных уравнений Da / sP / s = \ n a. (92.18)
Величина A является инвариантом тензора кривизны. по Поскольку след Daa = 0, сумма корней также равна нулю. Уравнение (92.18): A + A (2) + A® = 0. По числу независимых собственного вектора Паз па мы приходим к следующей классификации возможных При приведении тензора кривизны к канонической форме Петрова I — III. I. Есть три независимых собственных вектора.
В то же время Квадрат папы не равен нулю и вращается соответственно Тензор Дап вместе с Ааром и Варом имеют диагональ 358 Уравнение гравитационного поля CH. запад сердце A-ol (3- Ба (3 = ■ \ 0 0 a (2) ‘ 0 0 _ A (1) ‘ AM «0 0 д (2) 0 0 —a (x) » (92.19) В этом случае тензор кривизны имеет 4 независимых инварианта та 1).
Комплексные инварианты A ^ 1), A ^ 2) выражаются алгебраически Лыжи через сложный скаляр: h = ± — {RiklmRiklm-iRiklmR Я 4 8 h = ^ (RikimRlmprRprih + iRikimRlmprRprik), (92.20) Где звездочка над буквой означает двойной тензор: * 1 Риклм = ~ — ^ ikpr- ^ 1t- Используя (92.19) для вычисления ii, / 2, это выглядит так: h = 1 (aW 2+ A (2) 2+ A (1) A (2)), 12 = 1 a (1) A (2) (A (1) + A (2)). (92.21) 3 2 Эти формулы могут быть использованы для расчета A ^ 1) и A ^ 2).
Ний Риким во всех системах отсчета. II. Есть два независимых собственных вектора. площадь Этого не может быть, потому что один из них равен нулю Считается направление оси координат. Тем не менее, вы можете Поместите его в плоскость x1x2. P2 = ini? ^ с-0. Соответствующее уравнение (92.18) D u + iDi2 = A, D22-iDi2 = A, Откуда D n = A-g / x, D22 = A + g / x, D12 = / x.
Комплексное число X = Xf + iXff является скаляром, Может быть изменено. Одинаковая / х величина с различными комплексными числами Любой поворот может быть связан с любым (ненулевым) Значение, поэтому вы можете рассмотреть его, не теряя общности Реальная вещь. В результате следующий стандарт Материал тензора типа А ар, Бар: / A ‘/ l 0 \ / A «- / l 0 0 \ Аа (3 = I M X O)? = (ОА «+ / хОj. \ 0 O -2A 7 \ 0 0 —2A «/ (92.22)
В этом случае есть только два инварианта X ‘и A’ ‘. В то же время (92.21), ii = A2, / 2 = A3, поэтому, если = III. Существует только один собственный вектор нуля Площадь. Все собственные значения A одинаковы, Следовательно, оно равно нулю. Решение уравнения (92.18) имеет вид D u = D22 = D12 = O, D13 = / l, сокращено до формата D 23-W какие / ОО / Д / 0 0 0 \ А a p = 0 0 0, B a p = I 0 0 A. (92.23) V / x 0 0 / V0 M ° /
В этом случае тензор кривизны не имеет инвариантов. И мы имеем дело со странной ситуацией: 4-пространство Изогнутый, но не возможный инвариант Мера его кривизны 1). Задача 1. Тензор кривизны Pa / s ^ b в трехмерном пространстве 2 место тензор Рар. Решения. Ищу Pap7 в форме PcxP’ub = ^ Q ‘7’ T / 3 <5 A a S ^ f / 3 ‘y H “A / 3 b ^ / a’u A / 3 ^ y ^ fa S 5
Удовлетворяет условию симметрии, где Аар симметричен Тензор, связь которого с Rar определяется упрощением, записывается Выражение по индексам А и 7. Таким образом Rotfi = A’Uar Aa [3] Aar = Ra (3-P ^ ocfi *> 4 И наконец: р PafijS = Paj ^ pS PaS ^ PjН «Р / З’у’Уас’уP ^ j ^ aSН» ~ (‘Уаб’У / З7’Уа’уУ / Зб’) • 2. Вычисляет тензорные компоненты Riklm и Rik для следующих метрик Тензор Гик диагональный. Решения.
Представьте ненулевой метрический компонент Тензор формы -I ig2 Fi, wo-1, wo, -1. Следующая формула получается путем расчета по формуле (92.1). Ненулевая компонента тензора кривизны: Ruik = eie2Fl (FitkFk, i + Fi ^ F ^ i-Fi ^ F ^ k-Ft,;, &)> iφkφI, Run = eie2Fl (FitiFiti-F2 {-Fi ^ j) + e; e2F * (FijFij-F2t-Fi, 1,1) — -ete2Fl ^ eieme2iFi- Fm) FitmFi, m, ifI tf1.1 (Там нет общего количества повторных индексов!).
Десятичный индекс Имеется в виду простое дифференцирование с соответствующими координатами. Упрощенный тензор двух индексов Rik = ^ (Fi, kFk, i + Fi, kFi, i-FitiFitk-Fititk), r fk, 1f1, к Rii = -F \ ^ — + л ^ я + eie ie2 (Fi-Fi) (Ft, iFi, i-F2t-F Mli-Fitl ^ Fm ,,)].
Смотрите также:
| Уравнения электродинамики при наличии гравитационного поля | Действие для гравитационного поля |
| Тензор кривизны в физике | Тензор энергии-импульса |

