Сформулируем без доказательства основные свойства степенных рядов.
Свойство 1: Сумма 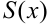 степенного ряда
степенного ряда  является непрерывной функцией в интервале сходимости
является непрерывной функцией в интервале сходимости 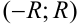 .
.
Свойство 2: Степенные ряды  и
и 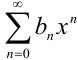 , имеющие радиусы сходимости соответственно
, имеющие радиусы сходимости соответственно 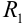 и
и 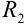 , можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из чисел
, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из чисел 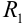 и
и 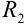 .
.
Свойство 3: Степенной ряд внутри интервала сходимости можно почленно дифференцировать. При этом для ряда 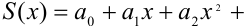
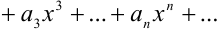 при
при 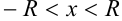 выполняется равенство
выполняется равенство 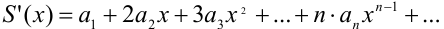
Полученный в результате дифференцирования степенной ряд имеет тот же радиус сходимости, что и исходный ряд.
Свойство 4: Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости. При этом для ряда 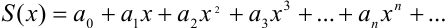 при
при 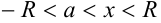 выполняется равенство
выполняется равенство
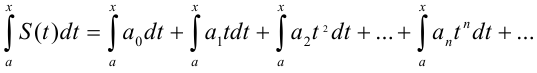
Полученный в результате интегрирования степенной ряд имеет тот же радиус сходимости, что и исходный ряд.
Свойства степенных рядов широко используются в теоретических исследованиях и в приближенных вычислениях.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие степенного ряда. Радиус и интервал сходимости. |
| Область сходимости степенного ряда. |
| Ряды Тейлора и Маклорена. |
| Разложение элементарных функций в ряд. |
