Оглавление:









Свойства равномерно сходящихся рядов и последовательностей
Свойства равномерно сходящихся рядов и последовательностей. Мы обнаружили, что сумма сходящихся рядов, в которых все члены являются непрерывными функциями, не может быть непрерывной функцией. Следующие теоремы содержат достаточные условия непрерывности для суммы рядов. itself. It уже не является набором какой-либо природы (до сих пор член рассматриваемого ряда, набор элементов последовательности и т.).) И по функциям, определенным на нем, должно быть таким, чтобы понятие непрерывности было defined. As для производных и интегралов класс допустимого множества Е следует еще более сузить.
Обратите внимание, что если вы рассматриваете непрерывную функцию в наборе, то на набор накладываются дополнительные ограничения. Людмила Фирмаль
- Теорема 8.Функции un (x), n-1, 2,…Если В точке x0 множества E A Cm) ряд 2 un (x) сходится равномерно В E его сумма e (x)= Y, un(x) также непрерывна с x^. Доказательство. Функции un (x), n = 1, 2,…непрерывны в точке x0 e E. докажем, что функция 5(x) также непрерывна в этом отношении. исправить e 0. Согласно гипотезам теоремы、 Следовательно, существует следующее число n8: Для всех x E и всех η>η, особенно для η=η.Функции sj (x), k = 1, 2, как сумма функций u (x) конечного числа…, так как n непрерывно в x0 e, существует 6 = 6 (e).Удовлетворяют условию p (x, x0) 6 для всех точек x∈E 6 Теперь, 5 (x)-«(x0)= [5 (x) § „E (x)] + [5“ e (x)) Здесь рассматривается комплекснозначная функция un (x), как и в любом другом месте, где больше ничего не указано. Понятие непрерывности таких функций см.
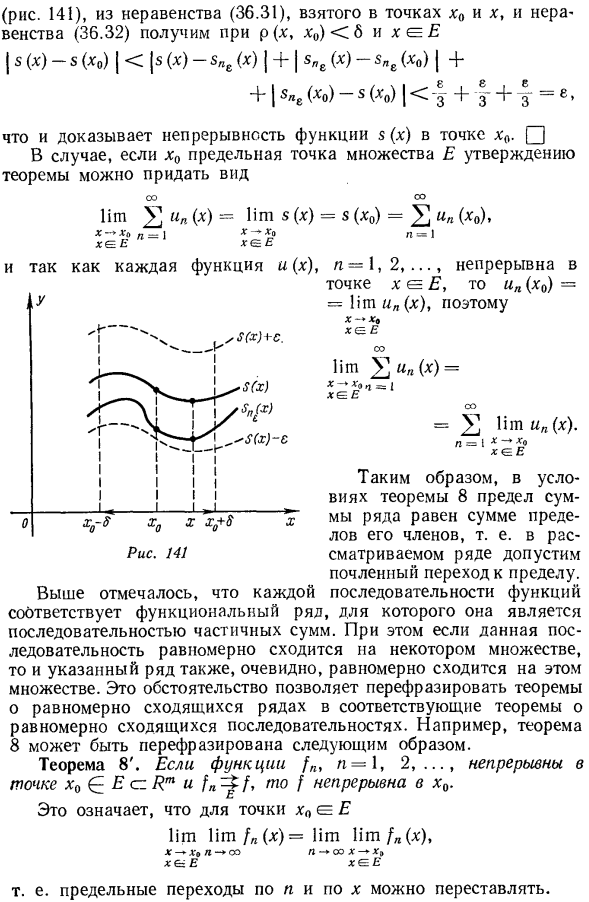
В разделе 23.3; обычно Pm обозначает м-мерное евклидово пространство. (Рис. 141), из неравенств, полученных в точках x0 и x (36.31) и неравенств (36.32), получаем около p (x, x0) 6 и x E Это доказывает непрерывность функции s (x) в x0. Если 0×0 является предельной точкой множества E, то описание теоремы дается следующим образом: И каждая функция u (x), n-1,2,…Что это?、 Точка X∈E, затем ООН(х0)=тηun (х), таким образом Итак, по условиям теоремы 8 предел суммы ряда равен сумме пределов его членов, то есть в рассматриваемом ряду допускается переход каждого периода к пределу. Выше было отмечено, что каждая последовательность функций соответствует функциональному ряду, в котором она является последовательностью частичных функций. sums.
- Кроме того, если определенная последовательность сходится равномерно к определенному множеству, то указанные ряды также сходятся к этому множеству четко и uniformly. In в этой ситуации теорему о сходящихся равномерно рядах можно назвать соответствующей теоремой о сходящихся равномерно последовательностях. Например, теорему 8 можно перефразировать следующим образом: 8’.Функция fn, n = 1, 2,…Если, смежно в точке x0∈C Km и{n^/, / смежно в точке x0. Для точки X » E ^ То есть вы можете переместить ограниченный переход на x в nn. Действительно, предел последовательности η= 1, 2/является функцией, непрерывной в точке x0 E, по теореме 8′, поэтому левая часть уравнения равна f (x0). Однако при непрерывности функции fn правая часть рассматриваемого уравнения также будет равна/(x0). Задача 25 (теорема Дини*’).
Функции η-1, 2…Предположим, что компактное тело (см) стремится к функции/если оно непрерывно, монотонно убывает или монотонно increasing. To докажите, что функция/непрерывна, необходимо и достаточно, чтобы последовательность{/}сходилась равномерно к множеству Å.Перефразируя этот результат серии. Далее мы переходим к вопросу о консолидации и дифференциации по терминам ряда. Во-первых, рассмотрим пример, который убеждает нас в том, что одной сходимости ряда функций недостаточно, чтобы найти Интеграл функции, равный ее сумме в терминах integrals. In другие слова.
Поскольку производные и интегралы определяются только в области вещественных чисел отсюда и до конца сечения, предположим, что все рассматриваемые функции определены на интервалах вещественной оси и принимают вещественные значения. Людмила Фирмаль
- Даже если ряды 2 un (x) и 2 ^и (x) Ax сходятся、 Даже если все записанные интегралы присутствуют, они могут быть ложными. Во-первых, мы перефразируем это утверждение с более поздней точки зрения. Доброе дело. $(х)= 2 un (х), 5н (х)= 2 ИК(х)、 У нас есть Покажите, что равенство Это не всегда так. Если существует предел Hm 8n (x) в интервале[a, b], и все рассматриваемые функции интегрируемы、 То есть в этом случае не всегда удается достичь предела под знаком интеграла. Допустим, 5 n (x)= nk-nk, n = 1, 2, 0,$ xc1.Тогда 5″(0)= 0 Использование ГФО. Часы hm5″(х)=0.Следовательно, 5 ″ ^ p. 0 и Таким образом, Интеграл предельной функции, то есть ноль, также будет равен нулю. Но Так что Mn \ 8n (x) Ax=〜, то есть фактически、 Последовательность{α, (x)}, неравенства 1 1 Когда вы строите серию из 2 un(x).
Смотрите также:

