Свойства пределов

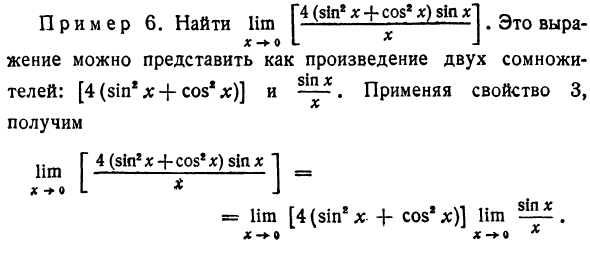
Свойства пределов

• Ограниченная собственность Во всех приведенных выше примерах никаких ограничений обнаружено не было, но такие числа оказались ограничениями для конкретной функции в указанных условиях. Естественно, возникает проблема того, как найти число, которое продолжает доказывать, что оно является пределом определенной функции.

Эта задача почти всегда Особенно сложно, исходя из определения ограничений. Представленные характеристики приведены в качестве примера, и никаких доказательств не приводится. Доказательства. Можно найти в более полном курсе. Например, Пискунов Н.С., «Дифференциальный интеграл» или Тарасов Н.П., «Курс высшей математики».

Ограничительные свойства обычно используются для облегчения этой задачи. Людмила Фирмаль

Свойство 1. Общий лимит для определенного числа функций равен сумме лимитов для каждой из этих функций, т.е. lim [f (x) + Φ ())] = lim f (x) + limlim (x). х а х а х а х а Формулировка этого свойства предполагает, что все пределы рассчитываются при одинаковых условиях, а именно: х ^ «4 ~ грех х Пример 1. Найти лим- X- * O X lim = 1 и lim * 2 = 0. х о х х — *> о х5-фсинкс т. Грех х Указано, потому что это –1 — Х х Недвижимость, мы получаем xs 4-sinx », sin * lim -! — = lim I xr- | — х о х х- * о [_ X = lim x1 + lim = 0 + 1 = 1.

Замечания. Формулировка свойства 1 относится к сумме, но, поскольку различие всегда можно описать как сумму, свойство 1 также распространяется на разницу. грех х х ^ Пример 2. Найти предел лим. X o * „Sinx — x9 sin * ,. —— = -—-}} (-x), поэтому примените свойство 1. Мы получаем sinx-x9 и fsin jc ,, 1h1 hm- = Ish- + (- = x- * o L l- »o L L J = lim lim (- * •) «1 + 0 = 1. X- ¥ 0 * X O

• Свойство 2. Ограничение функций для сохранения Это же значение равно этому значению. Формат этого свойства другой: постоянные ограничения Равен этой константе. Пример 3. Найти предел lim [sin’x + cos2 *]. Я Х- 2 Потому что любое значение x sin * x + cos1 x равно 1 Тогда функция может сохранить Постоянная, поэтому lim [sin1 * + cos1 x] = 1. Я Пример 4. Найти предел лимита 7.5. 7.5 или позже X-EAR Это нормально, независимо от x>, а lim 7.5 = 7.5. X т Свойство 3.

Б-г сим 1- хг грех х + грех * х Пример 5. Найти предел lim—j-. Х о х Пример 1 в этом разделе показал, что lim + sin * = 1 и §2, что lim = 1. Х х х х Недвижимость 3, получить \ t грех x + sin2 x _ fx * + грех x грех xl __ x- + Q x2 x- »o L x x J е. ** — fsinx slnx-t, = lim —— lim- = L = 1. X O X X Q X При формулировке свойства 3 упоминаются только две функции, но можно использовать одно и то же свойство для большего числа факторов.

Предел произведения двух функций равен произведению пределов этих функций. Людмила Фирмаль

t-r tj .. r4 (sin * x + cos * x) sin * l 0 Пример 6. Поиск lim I —-1-L-. Это L × J Используя [4 (sin2 x + cos1 *)] и свойство 3, это можно выразить как произведение следующих двух факторов: ct g 4 (sin2 x + cos’s) sinx «1 L * J ~~ = lim [4 (sin2 x + cos2 x)] lim-. X- + 9 X- + Q X При применении того же свойства к первому элементу, это выглядит так lim [4 (sin2 x + cos2 x)] lim- Х о х о х = lim 4 lim (sin2 x + cos2 x) lim ^^ = 4-1-1 = 4. X O X O X O X Свойство 4. Коэффициент отношения двух функций равен коэффициенту, полученному делением предела делителя на предел делителя.

Однако предел делителя не равен нулю. Пример 7. Найти предел lim —m. X т х 1 Так как lim (* + 2) = 4, lim (x-1) = 1 в свойстве 4 х — * — г х- * х У нас есть I- * + 2 4 A lim-r = -r- = 4. Если предел делителя равен нулю, частное ограничение может быть любым числом в зависимости от дивиденда. Вот пример: о Пример 8. Рассмотрим предел lim —j-. Где m является целым числом X o * Число> 0. В этом примере limx * = lim l: • lim l: • lim l: = 0, поэтому предел делителя равен нулю. Х 0 Х 0 Х 0 Х 0 Проанализируйте возможные частные случаи. Если m = 1, lim-9-lim-2 = lim-> lim- = cx> X- + Q X X- + Q X X- * 0 X X-> 0 X (См. Описание символа oo в пр.5§1 и пр.2§3).

Когда m = 3, lim-r = lim a = a. X- + O L * O Ох * Когда m = 5, lim-7 = lim ax * = lim x * = 0. Y * DG-> ОXО — ►о Поиск предела отношения двух функций, когда оба делителя и пределы дивиденда равны нулю, является наиболее частой и теоретически одной из наиболее важных проблем. Пожалуйста, будьте осторожны. Однако свойство 4 в этом случае бесполезно. Свойство 5 (ограничить важное свойство). Когда точка M движется произвольно вдоль оси Ox} и приближается к точке P

До этого предела точка P не совпадает с началом координат, поэтому возможны только два случая. 1) Если P имеет положительную абсциссу, то некоторое время точка M также имеет положительную абсциссу. 2) Если P имеет отрицательную абсциссу, то точка M из точки имеет отрицательную абсциссу. Отсюда: Если лимит не равен нулю, указатель предела некоторое время соответствует значению предела.

Смотрите также:

Предмет высшая математика

Исследование функции sin* при значениях	Предел lim (1+jc)*. Число e
Определения предела	Непрерывные функции