Оглавление:
Свойства определителей матриц
Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.
Свойство 1. («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот.
Иными словами,
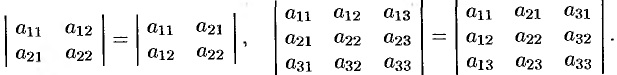
В дальнейшем строки и столбцы будем просто называть рядами опре-
делителя.
Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.
Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.
Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
Действительно,
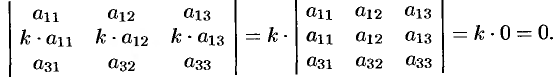
Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложев на сумму двух соответствующих определителей.
Например,
Свойство 6 («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.
Пример №2.3.
Доказать, что
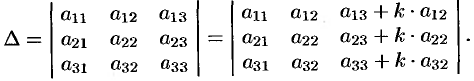
Решение:
Действительно, используя свойства 5, 4 и 3, получим
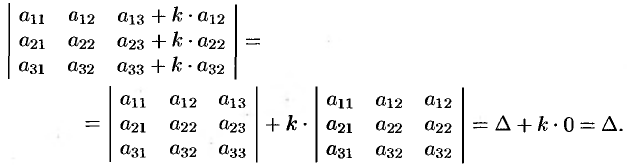
Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.
Минором некоторого элемента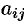 
определителя 
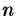-го порядка называется определитель 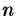— 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается 
.
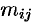Так, если
, то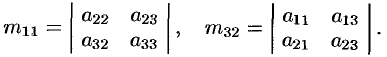 
Алгебраическим дополнением элемента 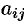определителя называется его минор, взятый со знаком «плюс», если сумма 
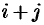— четное число, и со знаком «минус», если эта сумма нечетная. Обозначается 
.
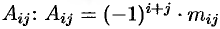Так,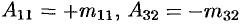 
.
Свойство 7 («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.
Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что
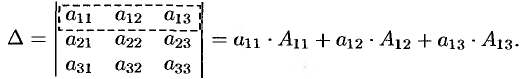
В самом деле, имеем
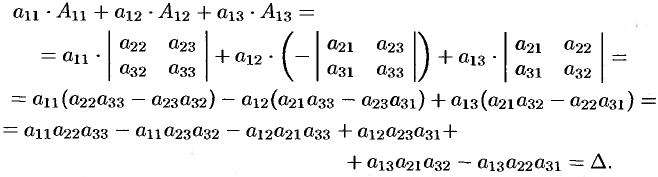
Свойство 7 содержит в себе способ вычисления определителей высоких порядков.
Дополнительный пример №2.4.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Произведение матриц |
| Невырожденные матрицы |
| Решение систем линейных уравнений |
| Операционный метод решения линейных дифференциальных уравнений и их систем |
