Свойства определителей с примерами

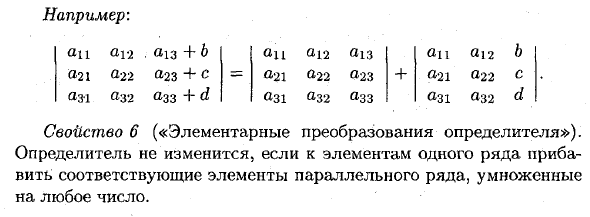
Свойства определителей

• ОПРЕДЕЛИТЕЛИ свойства Сформулируйте основные характеристики определителя, характерные для всех определителей степени. Некоторые из этих свойств описываются определителями третьего порядка. Свойство 1 («эквивалент строки и столбца»). Если строка заменяется на столбец, определитель не изменяется. Другими словами. «II» 21 «31» 12 «22» 32 «13» 23 «33 «А» 12 «11» 21 「21」 22 「12」 22 5 a p a \ 2 «13» 21 «22» 23 «31» 32 «33 В будущем строки и столбцы будут просто называться детерминантными строками.

Свойство 2. Свойство 3. Определитель с двумя одинаковыми рядами равен нулю. Свойство 4 • Общие факторы любого элемента строки определителя могут быть получены по признаку определителя. Из свойств 3 и 4 такой определитель равен нулю, если все элементы определенного ряда пропорциональны соответствующим элементам параллельного ряда.

Перестановка двух параллельных строк меняет знак определителя. Людмила Фирмаль

Пример: = B0 = 0. «11» 12 «13 Ail» 12 £ • «11 к-ай к • ай = к-« 11 «12 «31» 32 «33» 31 «32 «13 Свойство 5. Если элемент ряда определителя является суммой двух слагаемых, определитель может быть разложен на сумму двух соответствующих определителей.«12.« 13 + b »21« 22 0,23 + al a32 »sz + d «11» 12 «13» 21 «22» 23 «31» 32 «33 В Д д 11 '' 21 31 «12» 22 «32 + Свойство 6 («Основные преобразования определителей»). Если соответствующий элемент параллельного ряда, умноженный на любое число, добавляется к элементу в одной строке, определитель не изменяется.

«11» 12 «13» И «12» 13 + ~ • «12 d = «21» 22 «23 =» 21 «22 a2z + k •» 22 «31» 32 «33» 31 «32» ЗЗ + к • «32 Фактически, используя свойства 5, 4 и 3, 「11」 12 「13 + k」 「12」 21 「22」 23 Н〜к • 「22」 31 「32」 33 + к • Дз2 «11» 12 «12» 21 «22» 22 «31» 32 «32 «А» 12 «13» 21 «22» 23 «31» 32 «33 = D + b0 = D + ~ Дополнительные свойства определителей связаны с понятием минорных и алгебраических дополнений.

• Миноры определенных элементов a и j кубического определителя являются квадратичными определителями, полученными из исходного определителя путем удаления строк и столбцов, которые пересекаются выбранными элементами. Обозначается мн. «11» 12 «13» 21 «22» 23 «31» 32 «33 「11」 13 「21」 23 Алгебраическое дополнение элемента а *, определитель является второстепенным. Если сумма r + j является четным числом, она получается со знаком плюс, а если эта сумма является нечетным числом, она получается со знаком минус. Аид уточнил. Следовательно, An = + mlb Az2 = -tp32 «22» 32 「23」 33 Следовательно, D = мн = t32 =

Свойство 7 («Расширить определитель до элементов определенного ряда»). Определитель равен сумме произведений элементов определенного ряда с соответствующим алгебраическим дополнением. Мы, например, = «11 • Все +» 12 • ^ 12 + «13 • Alt- Ха и «12» 1z ~; 「21」 22 「23」 31 「32」 33 D = -4 на самом деле «N • Mx +« 12 • Л124- «13 • A \ z = «22» 23 + «12 •» 21 «23 ^ +» 13 • «21» 22 「32」 33 Azz «31» 31 «32 = «11 (» 22 «33-» 23 «32) -» 12 (021 «33-» 23 «3л) +» 13 («21» 32- «» 22 «3л) = =» П «22» 33- ~ «А» 23 «32 ~» 12 «21» 33+ «12» 23 «31 + + «13» 21 «32-» 13 «22» 31 = D. ► Характеристика 8. Сумма произведений элементов любого ряда в определителе алгебраическим дополнением соответствующих элементов параллельного ряда равна нулю. Так, например, A21 + 12- ^ 22 + 13L23 = 0.

Смотрите также:

Предмет высшая математика

Движение точки на плоскости. Система дифференциальных уравнений	Матрицы (основные понятия)
Определители (основные понятия)	Действия над матрицами