Рассмотрим основные свойства определенной) интеграла, считая подынтегральную функцию интегрируемой на отрезке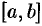 
. При выводе свойств будем использовать определение интеграла и формулу Ньютона-Лейбница.
1. Если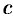 
— постоянное число и функция 
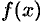интегрируема на 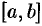, то
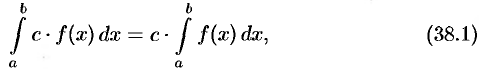
т. е. постоянный множитель 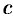можно выносить за знак определенного интеграла.
Составим интегральную сумму для функции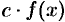 
. Имеем:
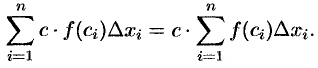
Тогда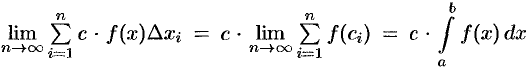 
. Отсюда вытекает, что функция 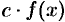интегрируема на 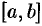и справедлива формула (38.1).
2. Если функци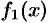и 
и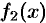 
интегрируемы на 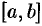, тогда интегрируема на 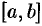их сумма и
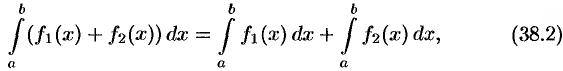
т. е. интеграл от суммы равен сумме интегралов.
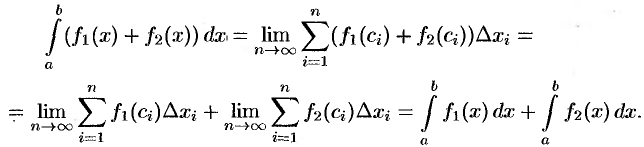
Свойство 2 распространяется на сумму любого конечного числа слагаемых.
3. 
.
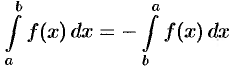Это свойство можно принять по определению. Это свойство также подтверждается формулой Ньютона-Лейбница.
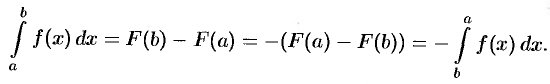
4. Если функция 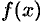интегрируема на 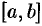и 
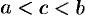, то
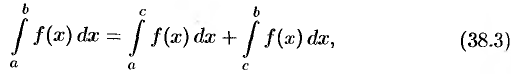
т. е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это свойство называют аддитивностью определенного интеграла (или свойством аддитивности).
При разбиении отрезка 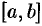на части включим точку 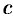в число точек деления (это можно сделать ввиду независимости предела интегральной суммы от способа разбиения отрезка 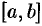на части). Если 
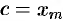, то интегральную сумму можно разбить на две суммы:
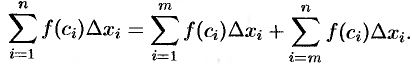
Каждая из написанных сумм является интегральной соответственна для отрезков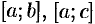 
и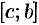 
. Переходя к пределу в последнем равенстве при 
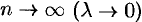, получим равенство (38.3).
Свойство 4 справедливо при любом расположении точек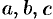 
(считаем, что функция 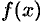интегрируема на большем из получающихся отрезков).
Так, например, если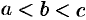 
, то
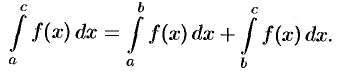
Отсюда
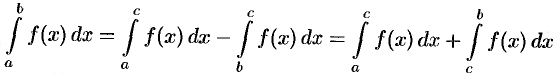
(использованы свойства 4 и 3).
5. «Теорема о среднем». Если функция 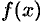непрерывна на отрезке 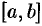, то существует точка 
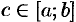такая, что
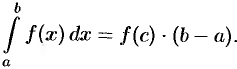
По формуле Ньютона-Лейбница имеем
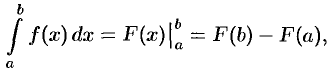
где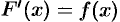 
. Применяя к разности 
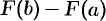теорему Лагранжа (теорему о конечном приращении функции), получим
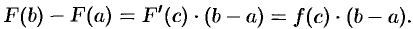
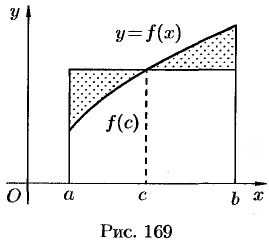
Свойство 5 («теорема о среднем») при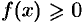 
имеет простой геометрический смысл: значение определенного интеграла равно, при некотором 
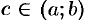, площади прямоугольника с высотой 
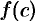и основанием 
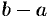(см. рис. 169). Число
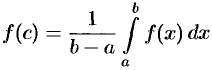
называется средним значением функции 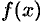на отрезке .
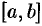6. Если функция 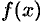сохраняет знак на отрезк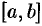е , где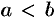 
, то интеграл 
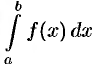имеет тот же знак, что и функция. Так, если 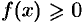на отрезке 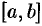, то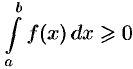 
.
По «теореме о среднем» (свойство 5)
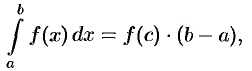
где 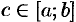. А так как 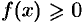для всех 
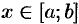, то и
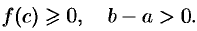
Поэтому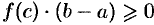 
, т. е. .
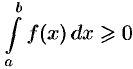7. Неравенство между непрерывными функциями на отрезке 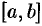, (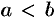) можно интегрировать. Так, если 
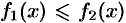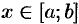при , то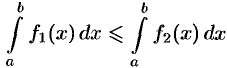 
.
Так как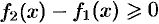 
, то при 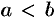, согласно свойству 6, имеем
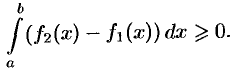
Или, согласно свойству 2,
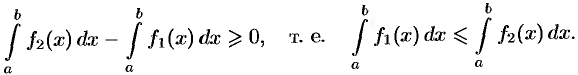
Отметим, что дифференцировать неравенства нельзя.
8. Оценка интеграла. Есл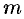и 
и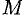 
— соответственно наименьшее и наибольшее значения фикции 
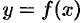на отрезке 
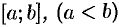, то
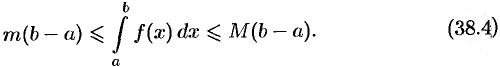
Так как для любого 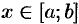имеем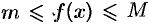 
, то, согласно свойству 7, имеем
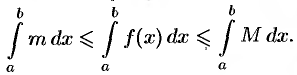
Применяя к крайним интегралам свойство 5, получаем
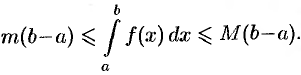
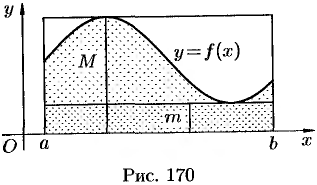
Если 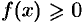, то свойство 8 иллюстрируется геометрически площадь криволинейной трапеции заключена между площадями прямоугольников, основание которых есть 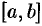, а высоты равны 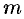и 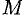(см. рис. 170).
9. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции:
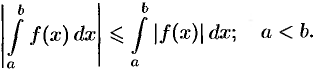
Применяя свойство 7 к очевидным неравенствам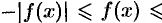 
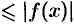, получаем
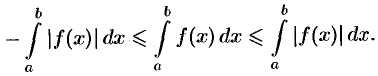
Отсюда следует, что
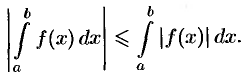
10. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом, т. е.
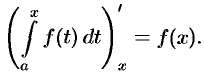
По формуле Ньютона-Лейбница имеем:
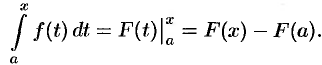
Следовательно,
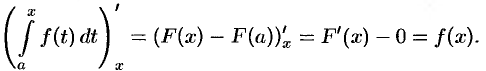
Это означает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Определенный интеграл как предел интегральной суммы |
| Геометрический и физический смысл определенного интеграла |
| Вычисления определенного интеграла |
| Интеграл с бесконечным промежутком интегрирования |
