Свойства нулевой линии
Перечислим свойства нулевой линии без доказательства.
- Нулевая линия никогда не пересекает тот квадрант, в котором приложена равнодействующая сила.
- Если точка приложения силы движется по прямой, пересекающей центр тяжести сечения, и приближается к центру тяжести, то нулевая линия смещается параллельно сама себе и удаляется от центра тяжести сечения.
- Если точка приложения силы находится на оси X (на оси F), то нулевая линия перпендикулярна оси Х(оси У).
- Если точка приложения силы движется по прямой, не проходящей через центр тяжести сечения, то нулевая линия поворачивается около неподвижной точки. Докажем это утверждение
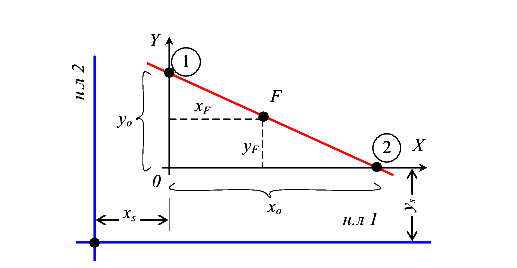
Пусть оси X и Y являются главными центральными осями инерции сечения. Поставим условие, чтобы точка приложения силы(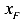 ,
,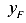 ) движется по прямой 1-2. Уравнение прямой 1-2 в отрезках имеет вид
) движется по прямой 1-2. Уравнение прямой 1-2 в отрезках имеет вид

Если сила приложена в точке 1, то нулевая линия будет перпендикулярна оси Y и удалена от оси Х на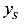

Если сила приложена в точке 2, то нулевая линия будет перпендикулярна оси X и удалена от оси У на 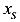 .
.

Вычислим напряжения в точке S при приложения силы в произвольной точке прямой 1-2.
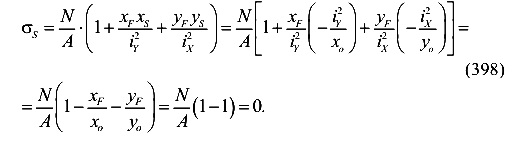
Таким образом, где бы не была приложена сила F на прямой 1-2, напряжение в точке S будет равно нулю. Следовательно, нулевая линия
при движении точки приложения силы F по прямой 1-2 будет поворачиваться около неподвижной точки S. Предположение доказано. Иллюстрация свойств нулевой линии приведена на рисунке 122.
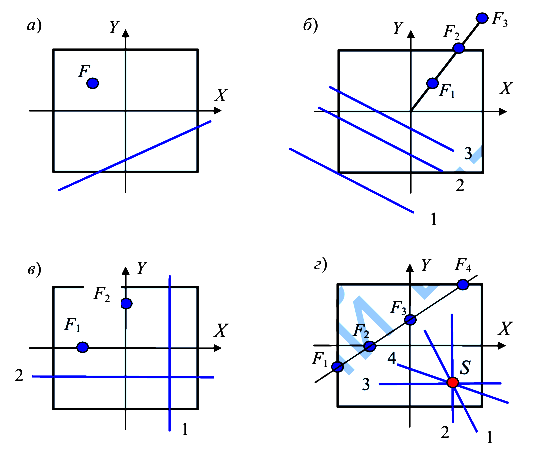
третье (в) и четвертое (г)
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Определение нормальных напряжений при внецентренном растяжении (сжатии) |
| Определение положения нулевой линии (нейтральной оси) при внецентренном растяжении (сжатии) |
| Ядро сечения |
| Свойства ядра сечения |

