Непрерывные на отрезке функции имеют ряд важных свойств. Рассмотрим одно из них.
Теорема 3.1 (Вейерштрасса). Если функция непрерывна на отрезке, тогда она достигает на нем своего наибольшего и наименьшего значения.
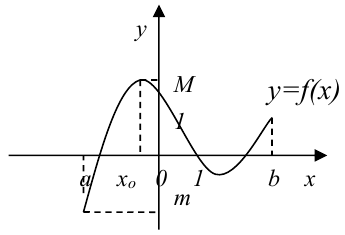
Изображенная на рисунке 10.3 функция непрерывна на отрезке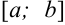 
. Наибольшее значение 
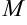функция достигает в точке 
, а наименьшее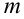 
— в точке 
.
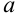Для любого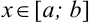 
имеет место неравенство: 
.
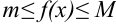Следствие. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Непрерывность функции в точке и на промежутке. |
| Основные теоремы о непрерывных функциях. |
| Непрерывность элементарных и сложных функций. |
| Точки разрыва, их классификация. |
