Оглавление:
Рассмотрим основные свойства рядов, опуская их доказательства.
Свойство 1. Если к ряду 
прибавить (или отбросить) конечное число членов, то полученный ряд сходится или расходится одновременно с данным. В случае сходимости рассматриваемых рядов их суммы отличаются на сумму добавленных или отброшенных членов.
Ряд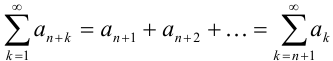 
называется 
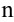-м остатком ряда , если он получен из данного ряда отбрасыванием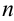 
его первых членов. В силу свойства 1 и определения остатка ряда, справедливы два следствия.
Следствие 1.1. Ряд и его остаток одновременно сходятся или расходятся.
Следствие 1.2. Если ряд сходится, то его остаток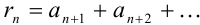 
стремится к нулю при 
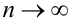, т.е. 
.
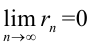С помощью этих следствий в некоторых случаях удастся оценить величину 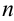-ого остатка ряда и тем самым оценить и точность приближения суммы ряда своими частичными суммами.
Свойство 2. Если ряд сходится, и его сумма равна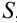 
, то для произвольного числа 
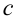ряд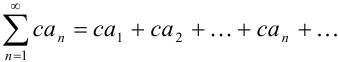 
также сходится, и его сумма равна 
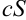. Если же ряд расходится и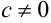 
, то и ряд 
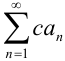расходится.
Свойство 3. Если ряды и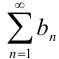 
сходятся, и их суммы равны 
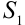и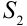 
соответственно, то сходятся и ряды 
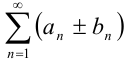, причем сумма каждого равна соответственно 
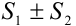. Другими словами: сходящиеся ряды можно почленно складывать и вычитать.
Из свойства 3 вытекают два следствия.
Следствие 3.1. Сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд.
Следствие 3.2. Сумма (разность) двух расходящихся рядов может быть как сходящимся, так и расходящимся рядом.
Обратимся к конкретным примерам использования свойств рядов при установлении их сходимости или расходимости.
Пример №32.4.
Исследуйте ряд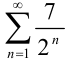 
на сходимость, применяя свойства рядов.
Решение:
Поскольку данный ряд получается из сходящегося ряда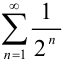 
(см. пример 32.3.) умножением на 
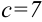, следовательно, согласно свойству 2 числовых рядов, он сходится.
Ответ: 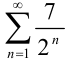сходится.
Пример №32.5.
Известно, что ряд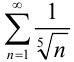 
расходится. Исследуйте ряд 
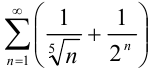на сходимость, применяя свойства рядов.
Решение:
Поскольку данный ряд представляет собой сумму сходящегося 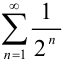(см. пример 32.3.) и расходящегося 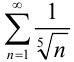рядов, значит, в силу следствия З.1., он расходится.
Ответ: 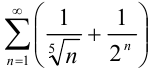расходится.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Вычисление площадей плоских фигур с помощью двойного интеграла. |
| Определение числового ряда. |
| Необходимый признак сходимости ряда. |
| Признак сравнения. |
