Свойства бесконечно малых величин представлены следующими теоремами.
Теорема 1. О связи между пределами и бесконечно малыми
a) Если переменная величина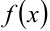 
стремится к конечному пределу 
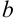, то разность между нею и её пределом есть бесконечно малая величина 
.
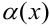б) Обратно, если переменная величина 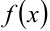равна сумме некоторой постоянной величины 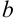и величины бесконечно малой, то эта постоянная величина есть предел переменной 
.
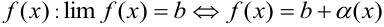Теорема 2. О сумме бесконечно малых величин
Алгебраическая сумма любого конечного числа бесконечно малых является бесконечно малой величиной.
Теорема 3. О произведении с бесконечно малой величиной
Произведение бесконечно малой на ограниченную функцию является величиной бесконечно малой.
Следствия теоремы:
- произведения бесконечно малых являются бесконечно малыми;
- произведение бесконечно малой и постоянной величины является величиной бесконечно малой;
- любая натуральная степень бесконечно малой — бесконечно малая.
Теорема 4. О связи бесконечно малых и бесконечно больших
Бесконечно большие функции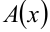 
и бесконечно малые 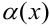связаны между собой равенством (при 
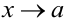или при 
)
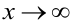Обратное равенство справедливо, если при изменении бесконечно малой 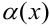она не принимает значений, равных нулю:
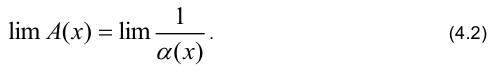
Условно связи (4.1) и (4.2) можно выразить так: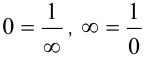 
.
Свойства бесконечно больших величин рассматриваются как следствия теорем 2, 3, 4 о бесконечно малых.
- сумма бесконечно большой и постоянной (или ограниченной величины
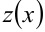) есть величина бесконечно большая; - произведение бесконечно большой и постоянной (или бесконечно большой) — величина бесконечно большая.
Условно указанные свойства можно выразить так: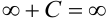 
; 
; 
; 
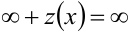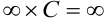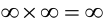. Иные случаи сочетания бесконечно больших и бесконечно малых функций, а именно, 
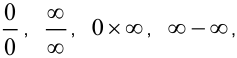называются неопределенностями. Раскрытие неопределенностей — основная сложность при вычислении пределов.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Предел функции при x>a |
| Предел функции при x>∞ |
| Свойства пределов в высшей математике |
| Кратко о двух замечательных пределов |
