Оглавление:
Свойства арифметических (алгебраических) корней
Пусть 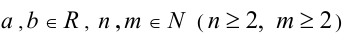
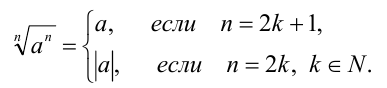
- если
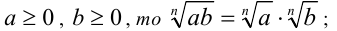
- если
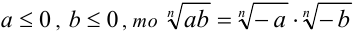
- (т.е. если
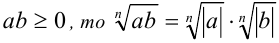 );
); - если
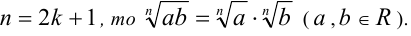
Дальнейшие свойства будут сформулированы для арифметических корней 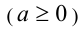 . Их можно обобщить на случай алгебраических корней аналогично тому, как это было сделано в данном пункте.
. Их можно обобщить на случай алгебраических корней аналогично тому, как это было сделано в данном пункте.
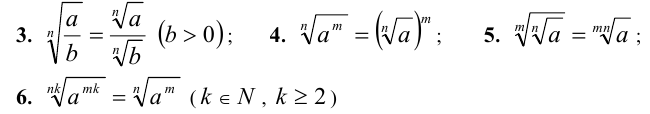
(если 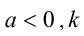 — чётное, то
— чётное, то 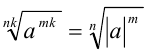 );
);
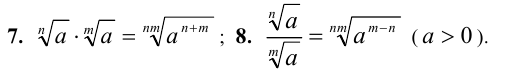
Доказательства этих свойств основаны на непосредственной проверке каждого из этих равенств, используя определения арифметического (алгебраического) корня и свойств степеней с целым показателем. Используется также тот факт (см. свойство 8б числовых неравенств), что два неотрицательных (неположительных) числа равны тогда и только тогда, когда их n -е степени (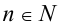 ) равны.
) равны.
Доказательство. 1. Пусть n = 2k + 1. Так как при любом действительном а числа 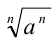 и а одного знака, то достаточно доказать, что после возведения данного равенства
и а одного знака, то достаточно доказать, что после возведения данного равенства 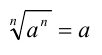 в степень n получим верное равенство
в степень n получим верное равенство 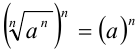 . Это действительно так, поскольку n -я степень левой части
. Это действительно так, поскольку n -я степень левой части
равенства 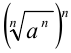 равна подкоренному выражению
равна подкоренному выражению 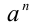 (по определению корня n -й степени), и n-я степень правой части равенства
(по определению корня n -й степени), и n-я степень правой части равенства 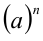 также равна
также равна 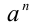 (по определению натуральной степени числа а ). Если же n= 2k , то свойство также верно, так как в этом случае
(по определению натуральной степени числа а ). Если же n= 2k , то свойство также верно, так как в этом случае 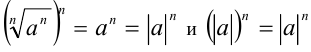 здесь при доказательстве использовалось свойство модуля
здесь при доказательстве использовалось свойство модуля 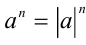 при чётных n ).
при чётных n ).
Остальные свойства будут доказаны для арифметических корней.
Пусть 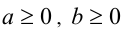 . Достаточно доказать равенство n -х степеней неотрицательных чисел
. Достаточно доказать равенство n -х степеней неотрицательных чисел 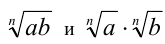 . Действительно,
. Действительно,  (по определению арифметического корня n -й степени). С другой стороны, по свойству 4 степеней с натуральными показателями имеем
(по определению арифметического корня n -й степени). С другой стороны, по свойству 4 степеней с натуральными показателями имеем
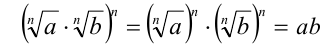
Пусть 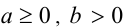 . Достаточно доказать равенство n-х степеней неотрицательных чисел
. Достаточно доказать равенство n-х степеней неотрицательных чисел 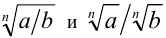 . Возведём проверяемое равенство в n -ю
. Возведём проверяемое равенство в n -ю
степень и, применяя для упрощения правой части свойство 5 степеней с натуральным показателем, а также используя для преобразования обеих частей определение арифметического корня n -й степени, получаем
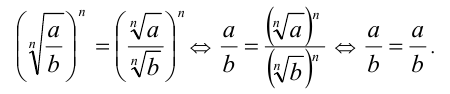
Возведём равенство в n -ю степень и, применяя для упрощения правой части свойство 3 степеней с натуральным показателем, а также используя для преобразования обеих частей определение арифметического корня, получаем
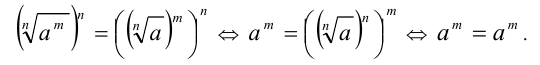
Возведём доказываемое равенство в mn -ю степень и, применяя в левой части свойство 3 степеней с натуральным показателем, получим
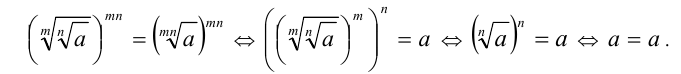
Возведём равенство в n —ю степень и воспользуемся только что доказанным свойством 5 арифметических корней (а также определением арифметического корня и свойством 3 степеней с натуральным показателем):
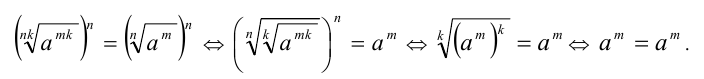
Возведём равенство в nm -ю степень и применим для упрощения левой части свойства 4, 3 и 1 степеней с натуральным показателем:
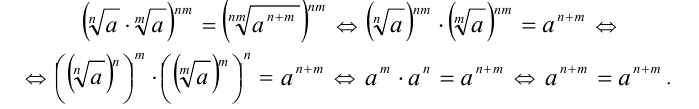
Возведём равенство в nm-ю степень и применим для преобразования левой части свойства 5, 3 и 2 степеней с натуральным показателем (а также в обеих частях равенства — определением арифметического корня):
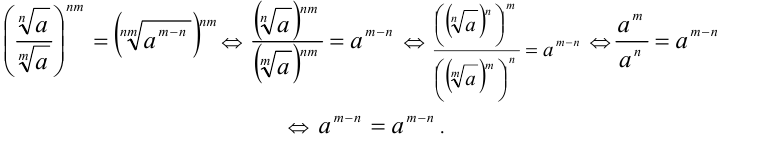
Пример №111.
Равносильны ли уравнения: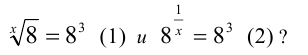
Решение:
1) Решим вначале второе из уравнений. Его ОДЗ задаётся неравенством 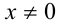 . Так как основание 8 степеней в обеих частях уравнения (2) одно и то же, то, приравнивая показатели степеней, приходим к уравнению
. Так как основание 8 степеней в обеих частях уравнения (2) одно и то же, то, приравнивая показатели степеней, приходим к уравнению 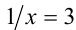 , откуда находим
, откуда находим 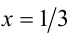 . Поскольку это значение принадлежит ОДЗ, получаем, что уравнение (2) имеет единственное решение
. Поскольку это значение принадлежит ОДЗ, получаем, что уравнение (2) имеет единственное решение 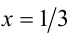 .
.
2) Решим теперь первое уравнение. Его ОДЗ задаётся условиями 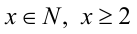 . Для решения уравнения перейдём к его следствию
. Для решения уравнения перейдём к его следствию 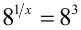 , решая которое по-прежнему находим
, решая которое по-прежнему находим 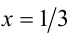 . Но в данном случае это значение уже не будет принадлежать ОДЗ уравнения (1), и поэтому не будет являться решением. Таким образом, приходим к результату: уравнение (1) не имеет решений. Ответ: уравнения не равносильны.
. Но в данном случае это значение уже не будет принадлежать ОДЗ уравнения (1), и поэтому не будет являться решением. Таким образом, приходим к результату: уравнение (1) не имеет решений. Ответ: уравнения не равносильны.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

