Абсолютно сходящиеся ряды занимают особое место среди знакочередующихся рядов, так как на такие ряды переносятся основные свойства конечных сумм. Приведем основные свойства абсолютно сходящихся рядов без доказательства.
Свойство 1 (теорема Дирихле): Если ряд абсолютно сходится, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму, что и исходный ряд.
Свойство 2: Абсолютно сходящиеся ряды с суммами 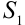 и
и 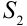 можно почленно складывать (вычитать). В результате получится абсолютно сходящийся ряд, сумма которого равна
можно почленно складывать (вычитать). В результате получится абсолютно сходящийся ряд, сумма которого равна 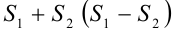 .
.
Свойство 3: Произведение двух абсолютно сходящихся рядов 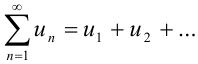 и
и 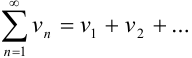 с суммами
с суммами 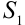 и
и 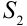 есть абсолютно сходящийся ряд
есть абсолютно сходящийся ряд 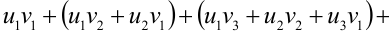
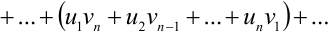 , сумма которого равна
, сумма которого равна 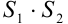 .
.
Для условно сходящихся рядов соответствующие свойства, вообще говоря, не имеют места.
Так, переставляя члены условно сходящегося ряда, можно добиться того, что сумма ряда изменится.
Более того, в силу теоремы Римана, путем перестановки членов условно сходящегося ряда можно получить сходящийся ряд с заранее заданной суммой или расходящийся ряд.
Поэтому действия над рядами нельзя производить, не убедившись в их абсолютной сходимости.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие знакочередующегося ряда. Признак Лейбница. |
| Абсолютная и условная сходимость знакочередующегося ряда. |
| Понятие функционального ряда. |
| Понятие степенного ряда. Радиус и интервал сходимости. |
