Оглавление:
Свободные колебания
Пусть материальная точка 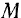 массы
массы 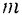 движется прямолинейно под действием силы
движется прямолинейно под действием силы 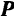 , направленной к неподвижному центру
, направленной к неподвижному центру 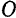 и пропорциональной расстоянию точки
и пропорциональной расстоянию точки 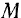 до этого центра. В начальный момент точка
до этого центра. В начальный момент точка 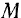 находилась от центра на расстоянии
находилась от центра на расстоянии 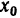 и имела скорость
и имела скорость 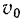 .
.
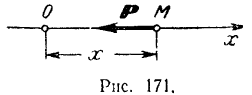
Определим движение этой точки.
Прямую, по которой движется точка, примем за ось 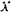 , взяв начало координат в неподвижном центре
, взяв начало координат в неподвижном центре 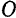 .
.
На точку 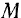 (изображенную на рис. 171 в произвольном положении) действует только сила
(изображенную на рис. 171 в произвольном положении) действует только сила 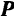 , модуль которой
, модуль которой
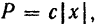
где 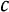 — некоторый постоянный коэффициент пропорциональности.
— некоторый постоянный коэффициент пропорциональности.
Силу 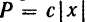 стремящуюся возвратить точку,
стремящуюся возвратить точку, 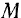 в положение равновесия, принято называть восстанавливающей силой. Эта сила при любом положении точки
в положение равновесия, принято называть восстанавливающей силой. Эта сила при любом положении точки 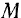 направлена к центру
направлена к центру 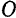 , следовательно, знак ее проекции на ось
, следовательно, знак ее проекции на ось 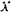 всегда противоположен знаку абсциссы
всегда противоположен знаку абсциссы 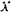 точки
точки 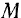 , и проекция
, и проекция 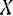 этой силы на ось
этой силы на ось 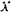 всегда будет равна —
всегда будет равна — 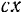 . Дифференциальное уравнение движения точки
. Дифференциальное уравнение движения точки 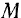 можно записать в виде
можно записать в виде
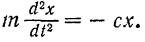
Переписав последнее уравнение в виде
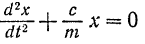
и обозначив постоянный положительный коэффициент 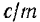 через
через 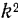 , получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
, получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
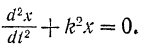
Для интегрирования его составляем характеристическое уравнение:
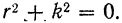
Корни этого уравнения
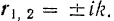
Как известно из теории дифференциальных уравнений, общее решение данного дифференциального уравнения имеет вид
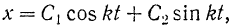
где 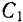 и
и 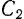 — постоянные интегрирования.
— постоянные интегрирования.
Данному решению можно придать более удобный вид, если ввести новые постоянные 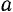 и
и 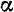 , положив:
, положив: 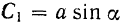 и
и 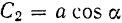 . Подставляя эти значения постоянных в уравнение (I), будем иметь:
. Подставляя эти значения постоянных в уравнение (I), будем иметь:
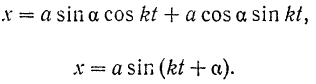
Как было сказано в кинематике (стр. 170), движение точки, совершаемое по подобному закону, называется гармоническим колебательным движением. Колебания точки, совершающиеся только под действием восстанавливающей силы, называются свободными или собственными колебаниями.
Таким образом, уравнение (116) является уравнением свободных колебаний точки под действием вое-станавливающей силы, пропорциональной расстоянию.
Важнейшей характеристикой колебательного движения служит период колебаний, т. е. время одного полного колебания.
Как было найдено в кинематике (формула (76)), период колебаний
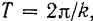
где 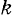 — круговая частота колебаний.
— круговая частота колебаний.
Так как при решении дифференциального уравнения движения (115) нами через 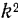 было обозначено отношение
было обозначено отношение 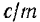 , то круговая частота свободных колебаний
, то круговая частота свободных колебаний
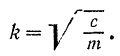
Следовательно, период свободных колебаний материальной точки
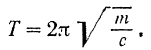
Как видно из формул (117) и (118), частота 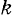 и период
и период 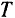 свободных колебании точки зависят только от массы этой точки и от величины коэффициента с пропорциональности в выражении восстанавливающей силы.
свободных колебании точки зависят только от массы этой точки и от величины коэффициента с пропорциональности в выражении восстанавливающей силы.
Величина 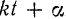 , стоящая в правой части равенства (116), называется фазой колебания точки, а величина
, стоящая в правой части равенства (116), называется фазой колебания точки, а величина 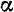 — ее начальной фазой.
— ее начальной фазой.
Постоянные 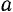 (амплитуда свободных колебаний) и
(амплитуда свободных колебаний) и 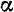 (начальная фаза колебаний) появились в уравнении (116) как результат замены в решении (I) постоянных интегрирования
(начальная фаза колебаний) появились в уравнении (116) как результат замены в решении (I) постоянных интегрирования 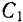 и
и 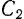 и определяются, следовательно, из начальных условий движения точки.
и определяются, следовательно, из начальных условий движения точки.
Дифференцируя по времени равенство (116), мы найдем алгебраическое значение скорости точки
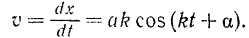
Подставляя начальные условия: при
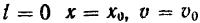
в выражение
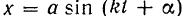

будем иметь
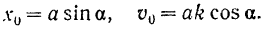
Решая совместно последние два уравнения относительно 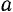 и
и 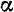 , находим
, находим
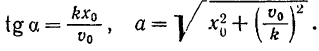
Пример задачи:
Груз 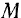 весом
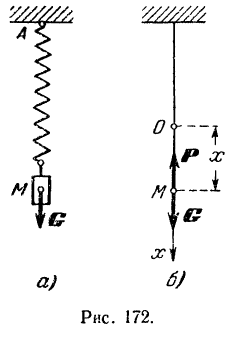
весом 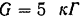 подвешен к пружине (рис. 172,а), конец которой
подвешен к пружине (рис. 172,а), конец которой 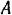 закреплен неподвижно. В положении статического равновесия удлинение пружины
закреплен неподвижно. В положении статического равновесия удлинение пружины 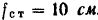 . Пренебрегая массой пружины и сопротивлением среды, определить закон движения груза. Сначала пружина была недеформирована и груз был предоставлен самому себе.
. Пренебрегая массой пружины и сопротивлением среды, определить закон движения груза. Сначала пружина была недеформирована и груз был предоставлен самому себе.
Решение:
Примем груз за материальную точку 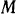 и направим ось
и направим ось 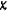 вертикально вниз (рис. 172,6). За начало
вертикально вниз (рис. 172,6). За начало 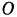 координат возьмем положение статического равновесия груза, соответствующее удлинению пружины на величину
координат возьмем положение статического равновесия груза, соответствующее удлинению пружины на величину 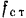 .
.
На груз действуют силы: 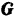 — сила тяжести груза и
— сила тяжести груза и 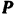 — сила упругости пружины. При отклонении груза
— сила упругости пружины. При отклонении груза 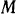 от положения статического равновесия (от начала координат
от положения статического равновесия (от начала координат 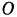 ) на величину
) на величину 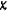 удлинение пружины равно
удлинение пружины равно 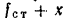 и модуль силы упругости пружины (восстанавливающей силы) равен
и модуль силы упругости пружины (восстанавливающей силы) равен 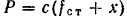 .
.
Коэффициент с пропорциональности (коэффициент жесткости пружины) легко находится из условия статического равновесия:
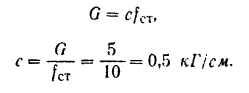
Составляем дифференциальное уравнение движения груза
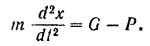
Подставляя в правую часть этого равенства значение
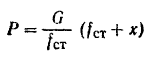
и сокращая обе его части на 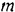 , получим:
, получим:
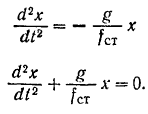
Сравнивая уравнение (I) с уравнением (115). видим, что груз совершает свободные гармонические колебания около положения статического равновесия по закону
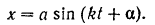
Круговая частота этих колебаний
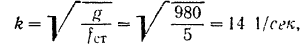
период колебаний
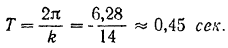
Амплитуда 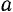 и начальная фаза
и начальная фаза 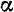 колебаний определяются из начальных условий. В нашем случае при
колебаний определяются из начальных условий. В нашем случае при
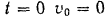
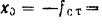
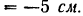
Подставляя эти данные в формулы (119), будем иметь:
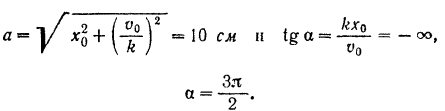
Таким образом, уравнение колебании груза принимает вид
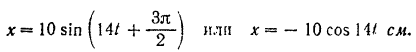
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

